Variety of Systems
Linear System
Systems that satisfy both homogeneity and additivity are considered to be linear system.
Homogeneity (scalar rule) means that as the strength of input signal is increased (scaled), then the strength of output signal will be also increased (scaled) with same amount.

Additivity denotes that the output of system can be computed as sum of the responses resulting from each input signal acting alone.

Taking these two rules together is called the principle of superposition. Therefore, the linear system can be presented as;

If input signal can be decomposed as a weighted sum of basis signals, the output of linear system is;

Examples
Determine if it is linear.
1) ![]()
sol>
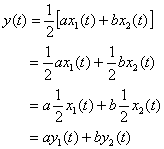
∴ linear system
2) ![]()
sol>
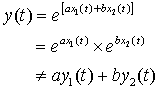
∴ non-linear system
Time-Invariant System
A system is time-invariant if a time shift in input signal causes an identical time shift in output signal.

Examples
Determine Time-Invariant.
1) ![]()
sol>
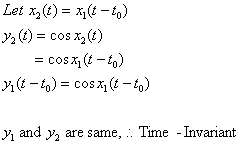
2) ![]()
sol>
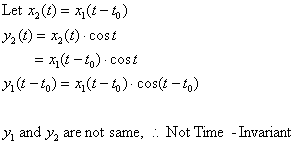
Causal System
A system is causal if the output at any time depends on values of the input at only the present and past times. In other words, the causal system does not anticipate future values of input.
For example, the output y(t0) depends on input x(t) for t ≤ t0.
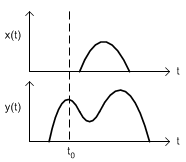
This is an example of non-causal system, because the output responds ahead at t = t0 before input is defined.
A causal system is characterized by an impulse response h(t) that is zeros for t < 0.
Examples
1) ![]()
Causal, because t ≥ t-2
2) ![]()
Non-Causal, because t ![]() t+1
t+1