Surface Area and Volume of Arbitrary 3D Geometry

Download: area.zip, volume.zip

• Surface Area of Triangle
• Surface Area of 3D Geometry
• Approximation Error
• Volume of Terahedron
• Volume of 3D Geometry
• Example

Surface Area of a Triangle

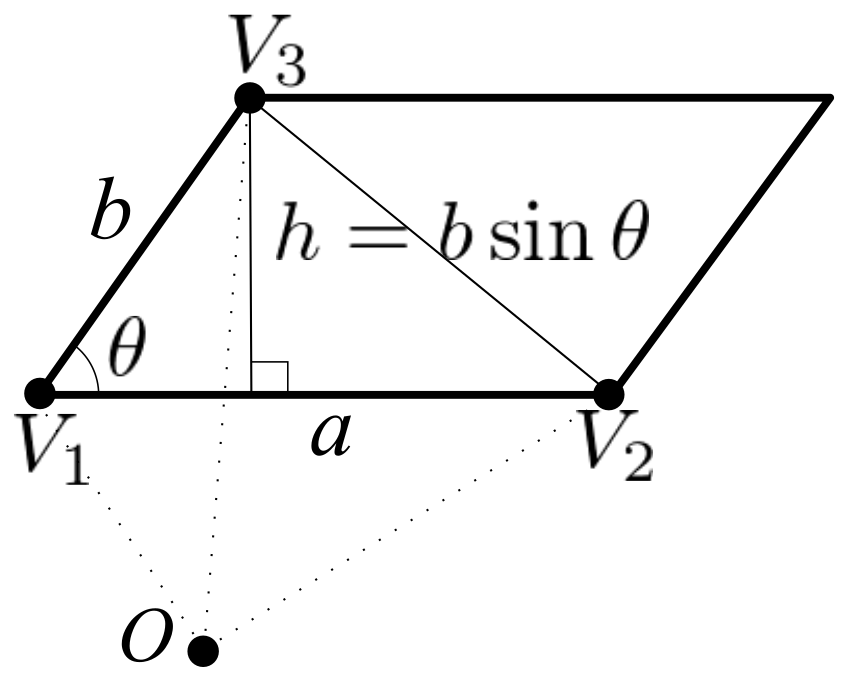
Suppose there is a single triangle V₁-V₂-V₃ in a 3D space. The surface area of this triangle is a half of the parallelogram constructed by V₁, V₂ and V₃.

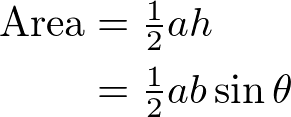
where a is the length of V₁-V₂, and b is the length of V₁-V₃.

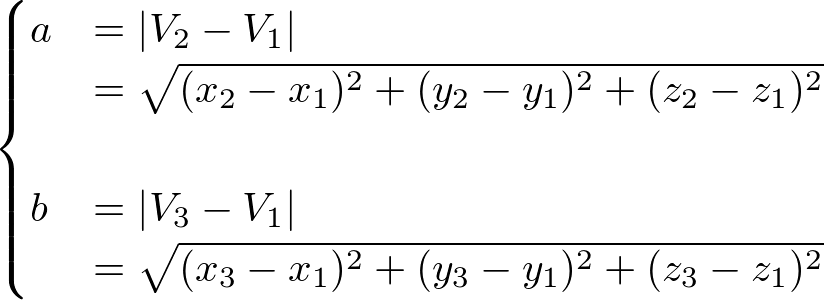
So, you can get the area by performing 2 square roots and sine function. But, there is a simpler formula using the cross product of 2 vectors.

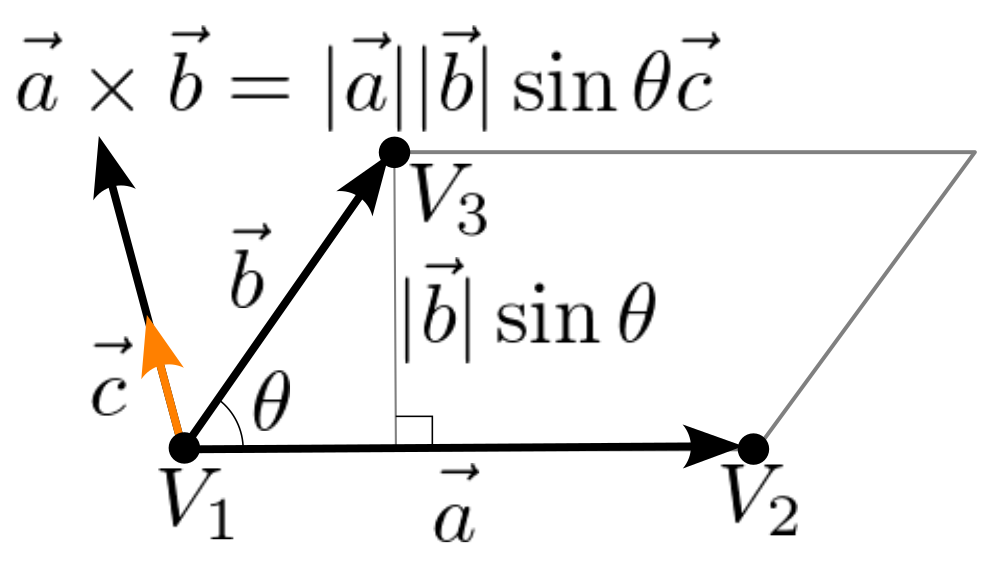
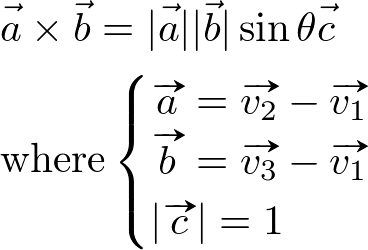
By definition of cross product, the magnitude of the cross product is equal to the area of parallelogram constructing 2 vectors.

The cross product is decomposed to a sum of 3 bases vectors and it's magnitude is

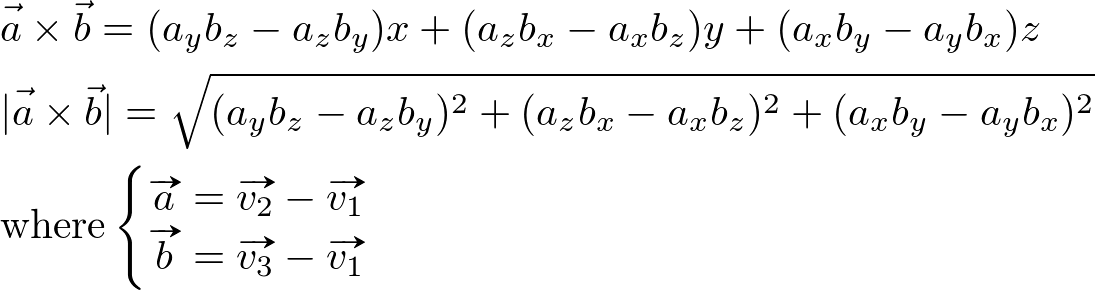
Therefore, the area of the triangle is a half of the parallelogram's area, which is the magnitude of the cross product.

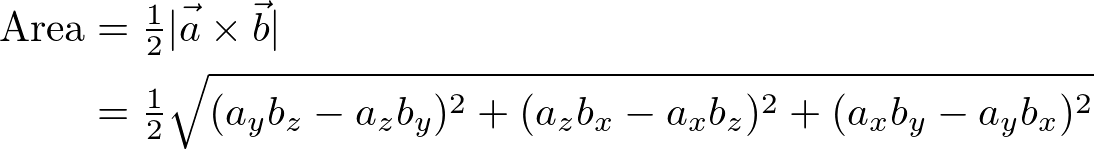
Surface Area of 3D Geometry

If an arbitrary 3D geomery is triangulated, the surface areas of the geometry is the sum of area of all triangles constructing the geomery.

If a geomery consists of N triangles, the total surface area is;

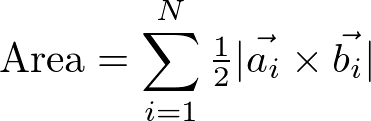
Here is C++ code snippet to compute the surface area of 3D geometry. The input parameters are an array of vertices, an array of indices and the number of indices for the geometry. See more detail in geomUtils.cpp file.

// calculate area of a single triangle
double computeTriangleArea(float v1[3], float v2[3], float v3[3])
{
    float v12[3];           // v2 - v1
    v12[0] = v2[0] - v1[0];
    v12[1] = v2[1] - v1[1];
    v12[2] = v2[2] - v1[2];
    float v13[3];           // v3 - v1
    v13[0] = v3[0] - v1[0];
    v13[1] = v3[1] - v1[1];
    v13[2] = v3[2] - v1[2];

    // v12 * v13 (cross product)
    double cross[3];
    cross[0] = v12[1]*v13[2] - v13[1]*v12[2];
    cross[1] = v12[2]*v13[0] - v13[2]*v12[0];
    cross[2] = v12[0]*v13[1] - v13[0]*v12[1];

    return 0.5 * sqrt(cross[0]*cross[0] + cross[1]*cross[1] + cross[2]*cross[2]);
}

// calculate area of a geometry
double computeArea(float* vertices, unsigned int* indices, int indexCount)
{
    double sum = 0;
    for(int i = 0; i < indexCount; i += 3)
    {
        float* v1 = &vertices[indices[i]  *3];
        float* v2 = &vertices[indices[i+1]*3];
        float* v3 = &vertices[indices[i+2]*3];
        sum += computeTriangleArea(v1, v2, v3);
    }
    return sum;
}

Approximation Error

Since a 3D geometry is represented with a limited number of triangles, there is an approxiamtion error. For example, the exact area of a sphere with its radius 1 is 12.56637061..., but the area of the sphere with only 1,000 triangles is 12.4654 (99.2% of the exact area). The following chart shows the approximation errors while the number of triangles increases. A sphere with 1M triangles is close to the exact area upto 4 decimal places.

Number of Triangles	Computed Area	Error	Accuracy
1,000 tris	12.4654	0.10095	99.1966%
5,000 tris	12.5439	0.02248	99.8211%
10,000 tris	12.5563	0.01009	99.9197%
50,000 tris	12.5642	0.00218	99.9826%
100,000 tris	12.5653	0.00104	99.9917%
500,000 tris	12.5661	0.00023	99.9982%
1,000,000 tris	12.5663	0.00010	99.9992%

Download the testing program to calculate the surface area and error for a sphere. You can increase the number of triangles by pressing SPACE key.
Download: area.zip

Volume of Tetrahedron

The volume of a parallelogram prism shape (or parallelepiped) is the product of the base area, A and its height, h, same as a cylinder. And, there are 6 equal-volume tetrahedrons inside the parallelogram prism.

Suppose there is a single triangle V₁-V₂-V₃. You can construct a tetrahedron and parallelepiped with these 3 points and an arbitrary point, e.g. the origin, O. The volume of this tetrahedron is defined by:

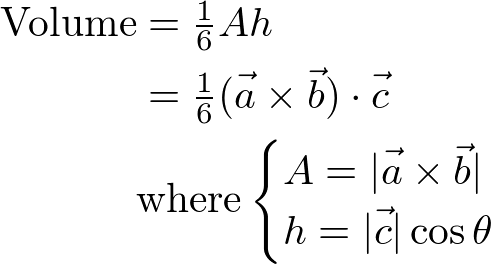
By definition of dot product, , the volume can be computed with . Or, it can be expressed using a matrix determinant notation as well.

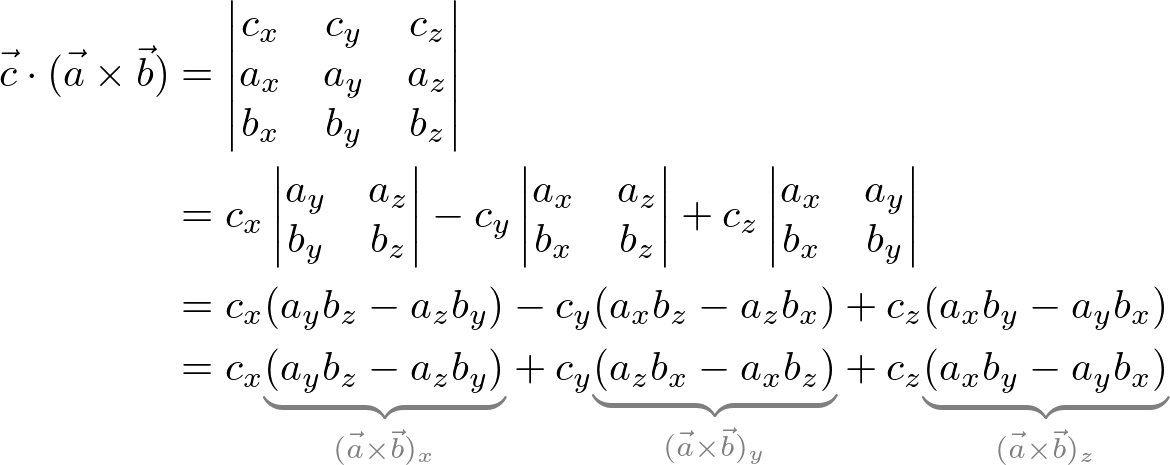
Volume of 3D Geometry

If an arbitrary 3D geomery with closed surface (no holes) is triangulated, the volume of the geometry is the sum of the volumes of all tetrahedrons constructed by triangles. If a geometry consists of N triangles, the total volume is;

Note that the volume of each tetrahedron is signed (can be negative). If a triangle normal is facing to the origin, the volume becomes negative. Therefore, the sum of all the volumes can cancel out outside of the geometry.

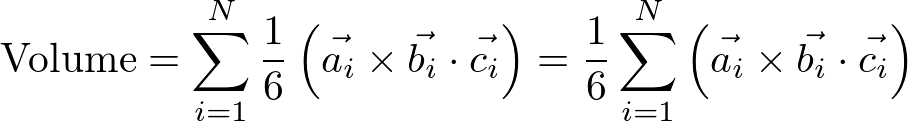
Let's visualize the volume calculation using a simple geometry. Suppose there is a unit cube positioned from (0,0,-1) to (1,1,-2). The cube consists of toal 6 faces or 12 triangles. The following diagrams shows the volume of each tetrahedron.

The front face are constructed 2 triangles; (0,0,-1)-(1,1,-1)-(0,1,-1) and (0,0,-1)-(1,0,-1)-(1,1,-1). And, the volumes of the tetrahedrons from the origin are:

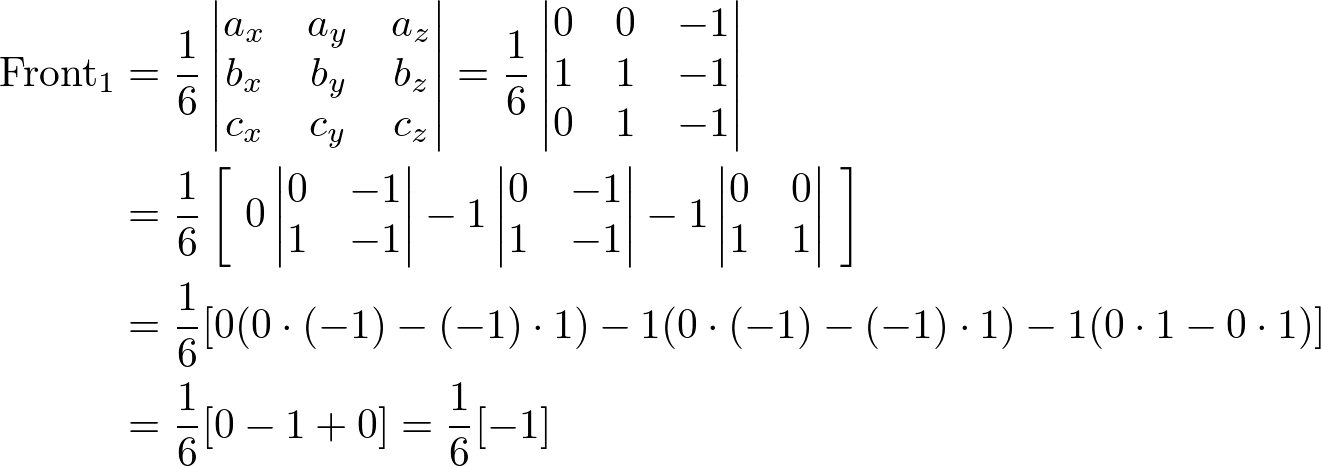
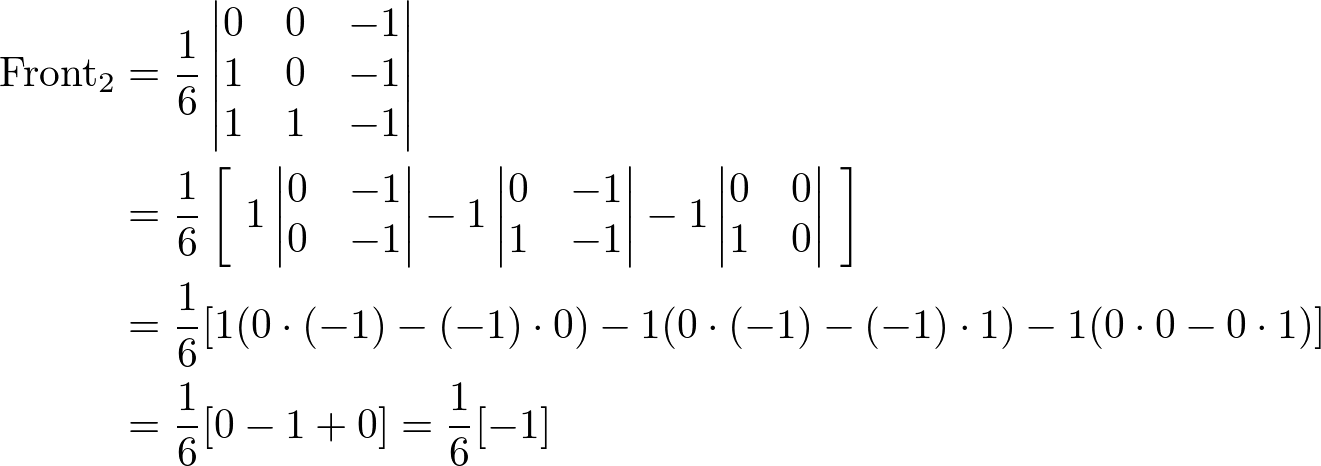
The right-side triangles are defined by (1,1,-1)-(1,0,-1)-(1,1,-2) and (1,0,-1)-(1,0,-2)-(1,1,-2). The volumes of right-side tetrahedrons are:

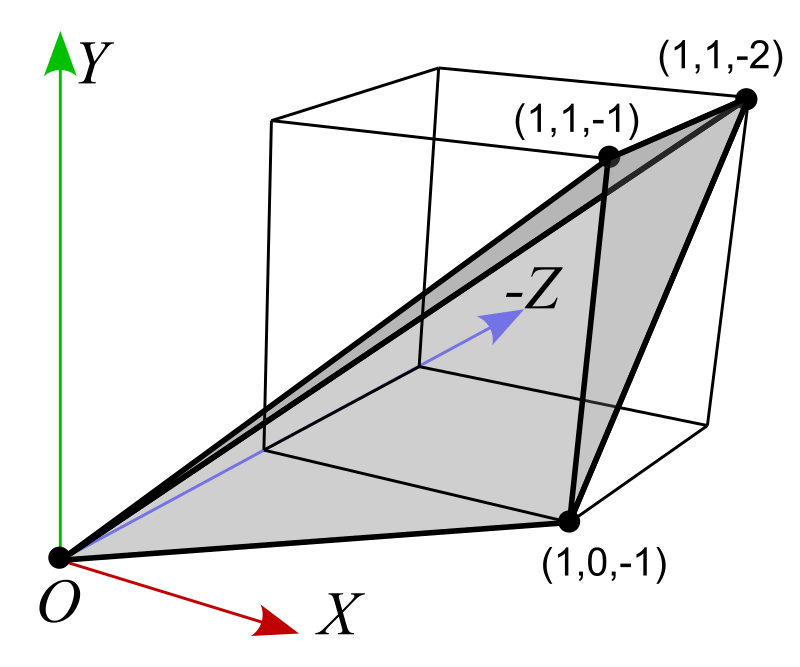
The top triangles are defined by (1,1,-1)-(0,1,-2)-(0,1,-1) and (1,1,-1)-(1,1,-2)-(0,1,-2). The volumes of top-face tetrahedrons are:

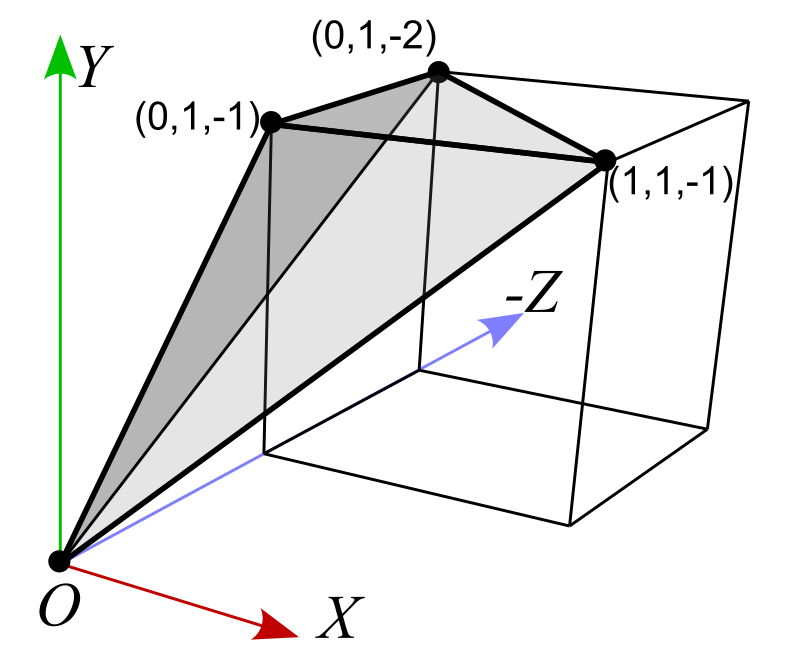
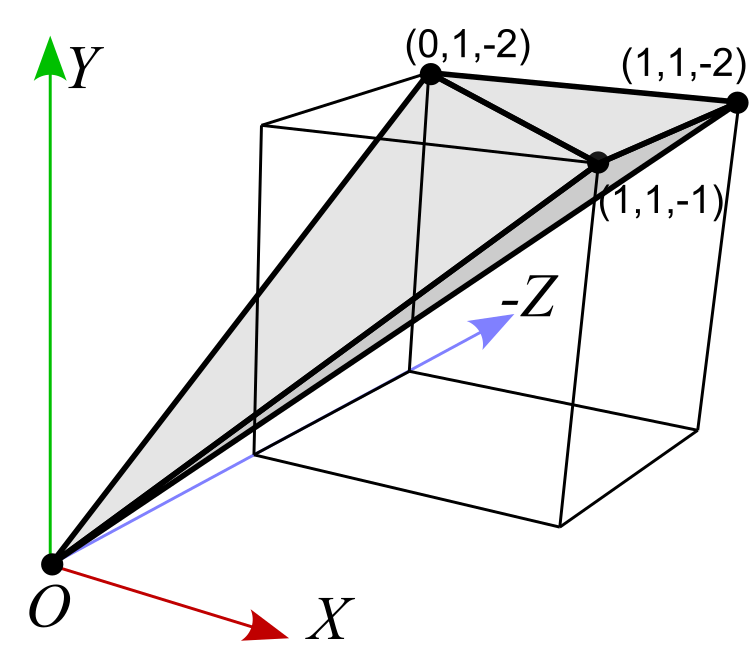
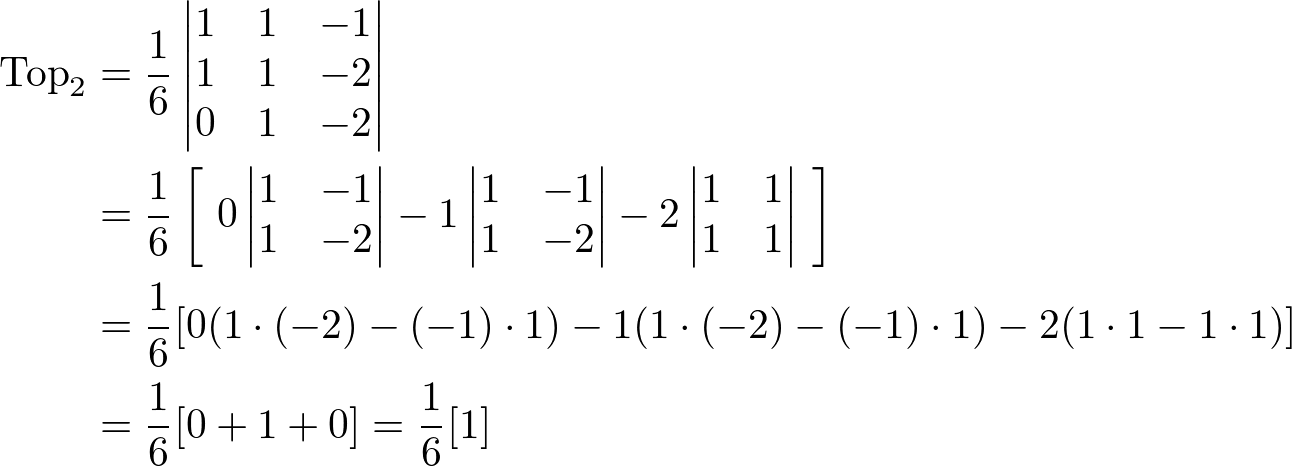
The back-side triangles are defined by (0,1,-2)-(1,0,-2)-(0,0,-2) and (0,1,-2)-(1,1,-2)-(1,0,-2). The volumes of back-face tetrahedrons are:

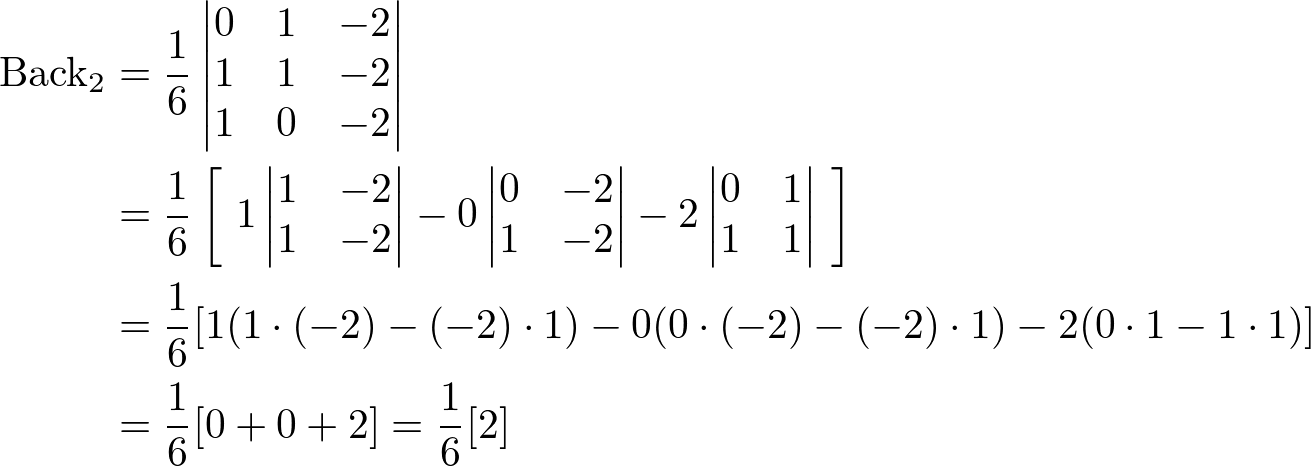
The left and bottom faces are on the same plane (the height of tetrahedron is 0), so the volumes are 0 for these faces.

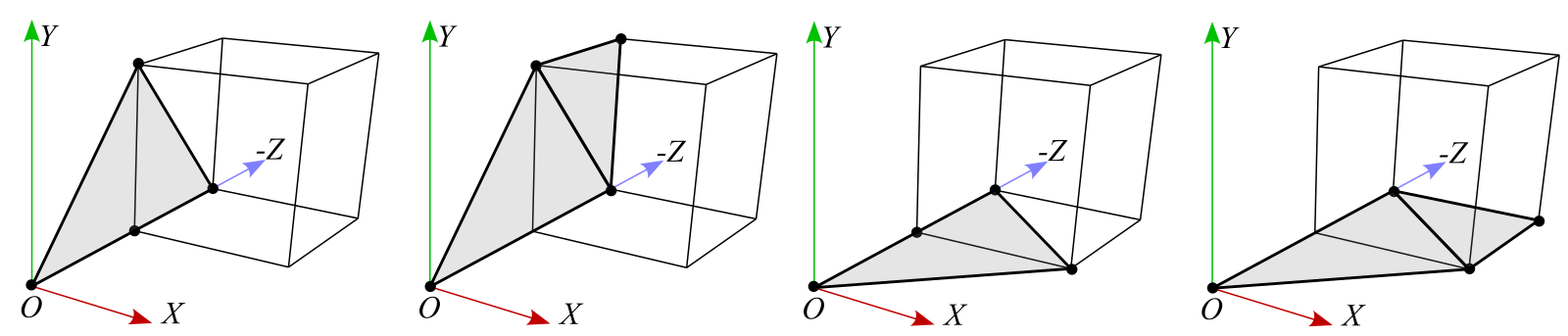
Therefore, the total volume of the cube is the sum of all tetrahedrons:

Example: Surface Area & Volume

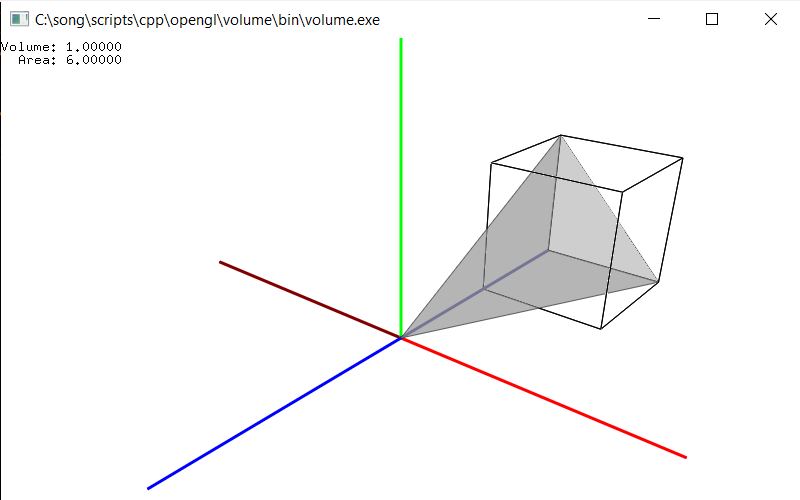
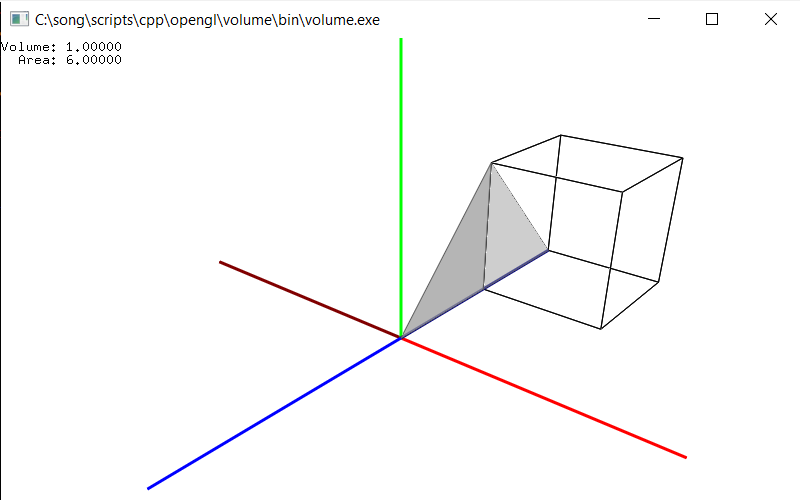
Download: volume.zip

This example loads an OBJ model and calculates the surface are and volume of the OBJ model. And, it visualizes the process of the volume calculations one by one. Please see geomUtils.cpp file ho the surface area and volume are computed.