OpenGL Cone & Pyramid
Related Topics: OpenGL Cylinder
Download: cone.zip, coneShader.zip
- Cone & Pyramid
- Apex Normal
- Example: Drawing Cone
- Example: WebGL Cone with Normals (Interactive Demo)
This page describes how to generate a cone or pyramid geometry using C++ and how to draw it in OpenGL.
Cone & Pyramid
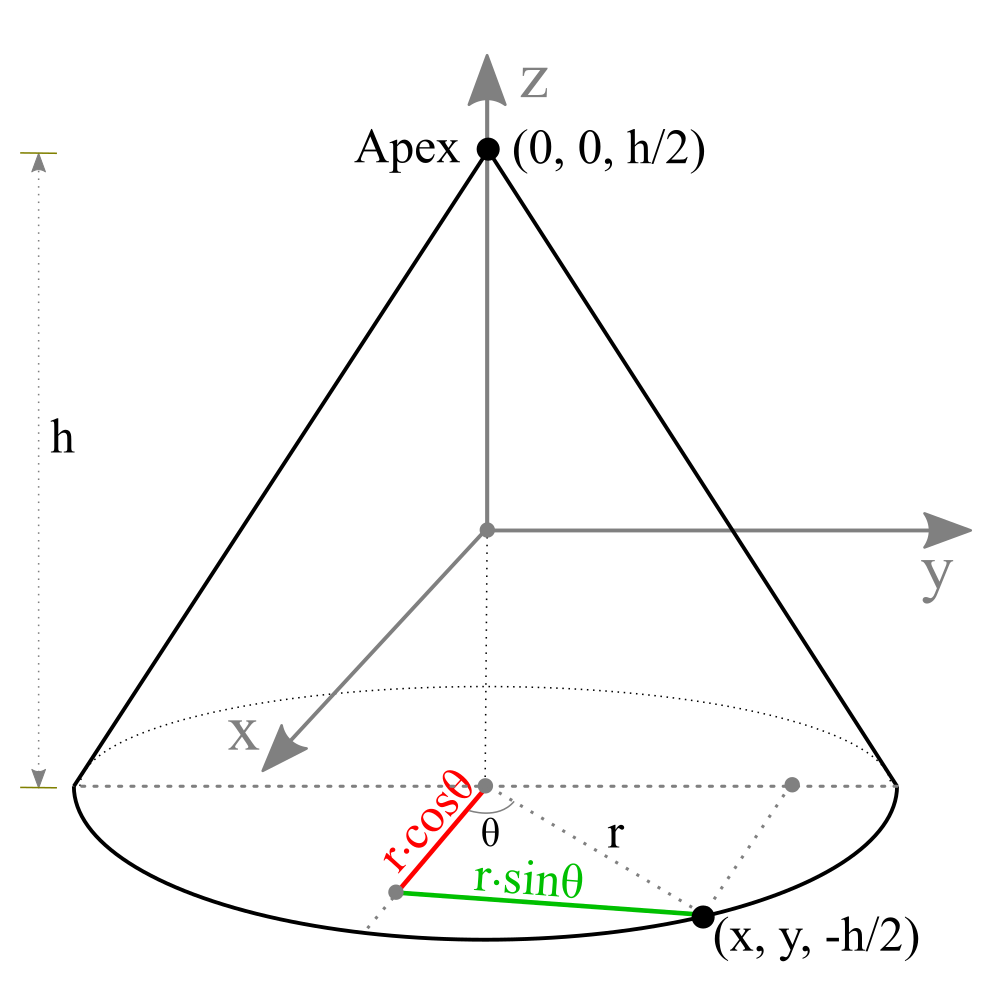
Drawing a cone is similar to drawing a cylinder. The only difference is that the top of a cylinder a flat circular surface, but the top of a cone geometry is a vertex (apex).
To construct a cone geometry, we need the radius of the base surface and the height of the cone. By assuming a cone is positioned at the origin and its axis is along Z-axis, the base vertices can be computed;
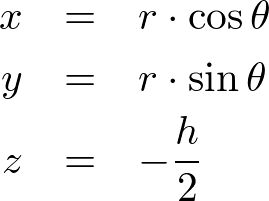
The sector angle for each step can be calculated by the following;
![]()
And, the apex vertex is on the Z-axis;
![]()
The number of sides (sectors) of a cone will determine the shape of the geometry; if the side count is 3, it becomes a tetrahedron, if the side count is is 4, then it is a square pyramid, and so on.
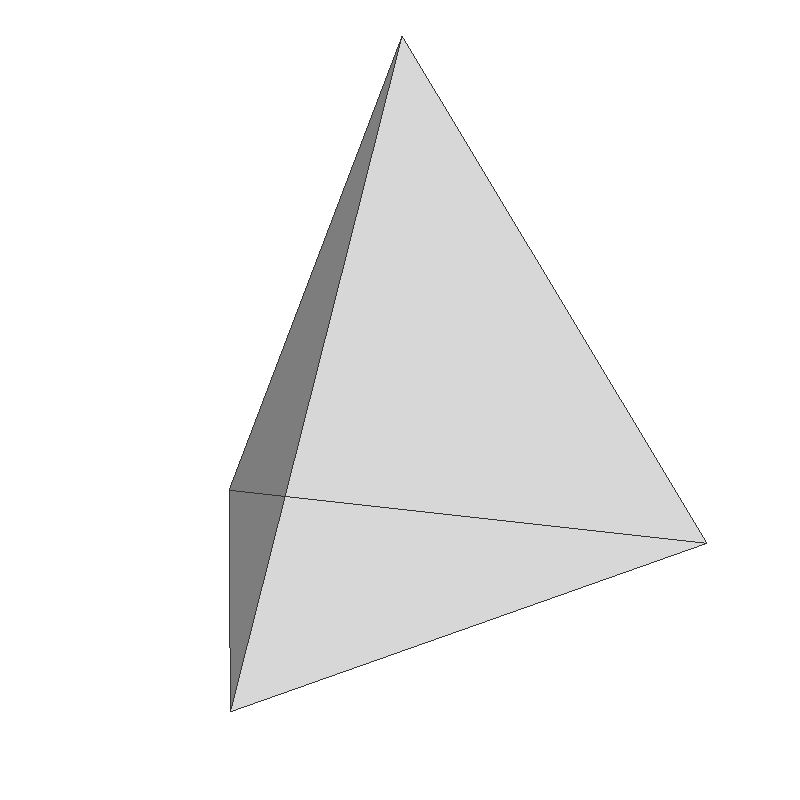
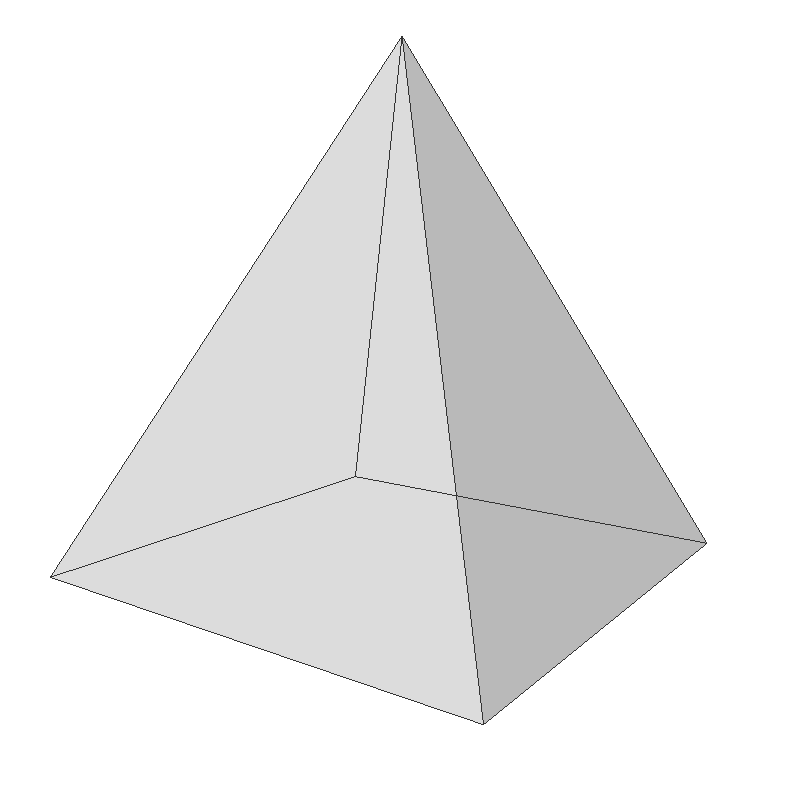
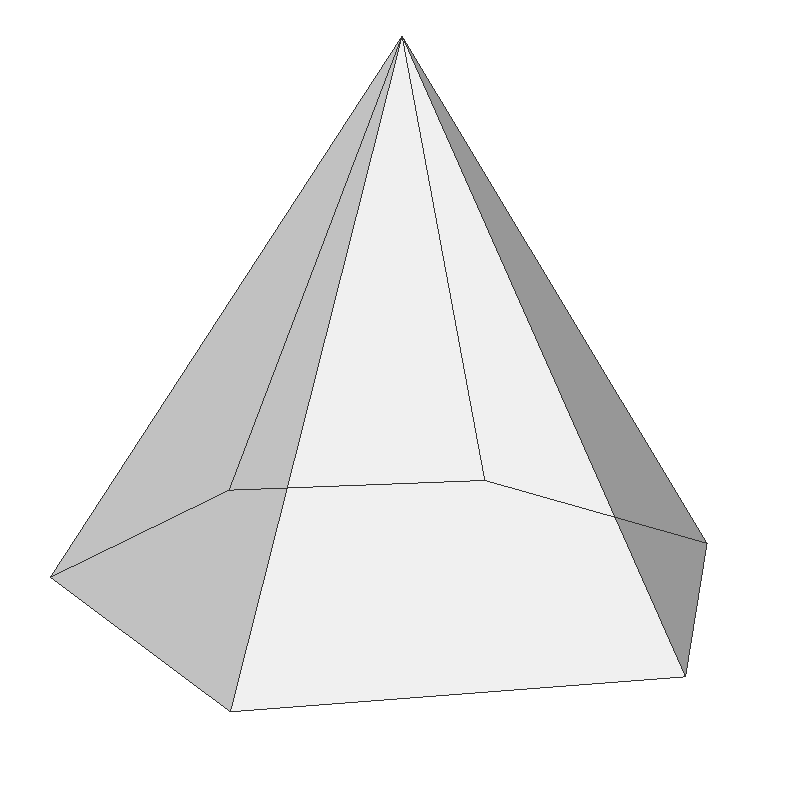
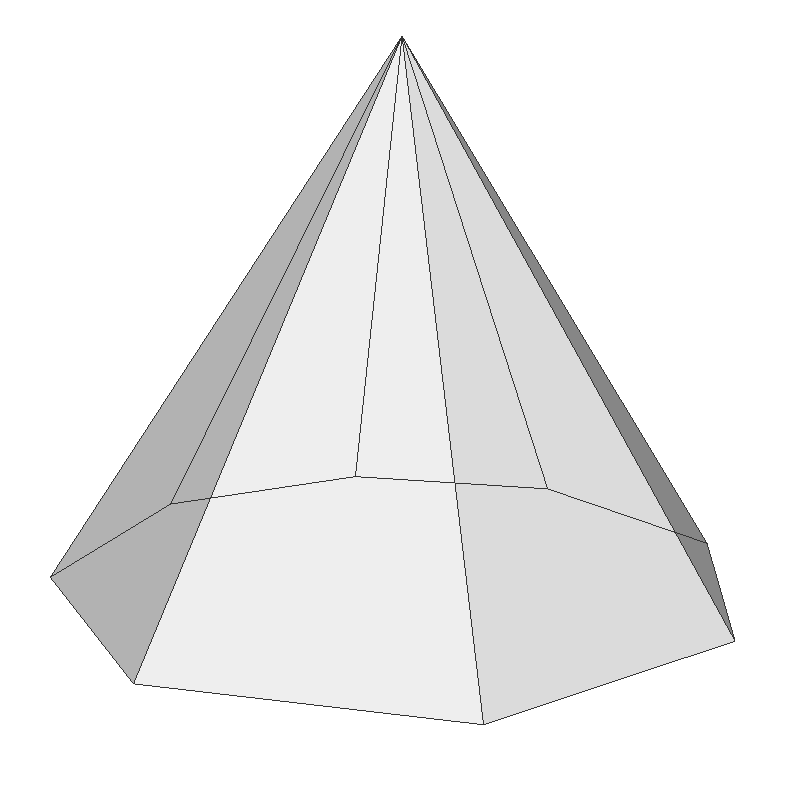
The following C++ code generates all vertices of the cone with the given base radius, height, and the number of sectors (sides) and stacks. It also creates other vertex attributes; surface normals and texture coordinates. For faster computation, it generates an vertices of a unit circle first, then scale them by the given radius.
// generate vertices for a cone
void Cone::buildVerticesSmooth()
{
float x, y, z; // vertex pos
float radius; // radius for each stack
// get normals for the sides
std::vector<float> sideNormals = getSideNormals();
// put vertices of side to array by scaling unit circle
for(int i = 0; i <= stackCount; ++i)
{
z = -(height * 0.5f) + (float)i / stackCount * height; // vertex pos z
radius = baseRadius * (1.0f - (float)i / stackCount); // lerp
float t = 1.0f - (float)i / stackCount; // top-to-bottom
for(int j = 0, k = 0; j <= sectorCount; ++j, k += 3)
{
x = unitCircleVertices[k];
y = unitCircleVertices[k+1];
addVertex(x * radius, y * radius, z); // position
addNormal(sideNormals[k], sideNormals[k+1], sideNormals[k+2]); // normal
addTexCoord((float)j / sectorCount, t); // tex coord
}
}
// remember where the base.top vertices start
unsigned int baseVertexIndex = (unsigned int)vertices.size() / 3;
// put vertices of base of cone
z = -height * 0.5f;
addVertex(0, 0, z);
addNormal(0, 0, -1);
addTexCoord(0.5f, 0.5f);
for(int i = 0, j = 0; i < sectorCount; ++i, j += 3)
{
x = unitCircleVertices[j];
y = unitCircleVertices[j+1];
addVertex(x * baseRadius, y * baseRadius, z);
addNormal(0, 0, -1);
addTexCoord(-x * 0.5f + 0.5f, -y * 0.5f + 0.5f); // flip horizontal
}
// put indices for sides
unsigned int k1, k2;
for(int i = 0; i < stackCount; ++i)
{
k1 = i * (sectorCount + 1); // bebinning of current stack
k2 = k1 + sectorCount + 1; // beginning of next stack
for(int j = 0; j < sectorCount; ++j, ++k1, ++k2)
{
// 2 trianles per sector
addIndices(k1, k1 + 1, k2);
addIndices(k2, k1 + 1, k2 + 1);
}
}
// remember where the base indices start
baseIndex = (unsigned int)indices.size();
// put indices for base
for(int i = 0, k = baseVertexIndex + 1; i < sectorCount; ++i, ++k)
{
if(i < (sectorCount - 1))
addIndices(baseVertexIndex, k + 1, k);
else // last triangle
addIndices(baseVertexIndex, baseVertexIndex + 1, k);
}
}
//===== Utility Functions =====
// generate 3D vertices of a unit circle on XY plance
void Cone::buildUnitCircleVertices()
{
const float PI = acos(-1.0f);
float sectorStep = 2 * PI / sectorCount;
float sectorAngle; // radian
std::vector<float>().swap(unitCircleVertices);
for(int i = 0; i <= sectorCount; ++i)
{
sectorAngle = i * sectorStep;
unitCircleVertices.push_back(cos(sectorAngle)); // x
unitCircleVertices.push_back(sin(sectorAngle)); // y
unitCircleVertices.push_back(0); // z
}
}
// generate shared normal vectors of the side of cone
std::vector<float> Cone::getSideNormals()
{
const float PI = acos(-1.0f);
float sectorStep = 2 * PI / sectorCount;
float sectorAngle; // radian
// compute the normal vector at 0 degree first
// tanA = baseRadius / height
float zAngle = atan2(baseRadius, height);
float x0 = cos(zAngle); // nx
float z0 = sin(zAngle); // nz
// rotate (x0,y0,z0) per sector angle
std::vector<float> normals;
for(int i = 0; i <= sectorCount; ++i)
{
sectorAngle = i * sectorStep;
normals.push_back(cos(sectorAngle)*x0); // nx
normals.push_back(sin(sectorAngle)*x0); // ny
normals.push_back(z0); // nz
}
return normals;
}
// add single vertex to array
void Cone::addVertex(float x, float y, float z)
{
vertices.push_back(x);
vertices.push_back(y);
vertices.push_back(z);
}
// add single normal to array
void Cone::addNormal(float nx, float ny, float nz)
{
normals.push_back(nx);
normals.push_back(ny);
normals.push_back(nz);
}
// add single texture coord to array
void Cone::addTexCoord(float s, float t)
{
texCoords.push_back(s);
texCoords.push_back(t);
}
// add 3 indices per triangle to array
void Cone::addIndices(unsigned int i1, unsigned int i2, unsigned int i3)
{
indices.push_back(i1);
indices.push_back(i2);
indices.push_back(i3);
}
This C++ Cone.cpp class takes 6 parameters; base radius, height, sector count, stack count, smoothness and up direction. And it provides buildVerticesSmooth() and buildVerticesFlat() functions depending on surface smoothness.
The parameters and default values of the Cone.cpp class are;
- Base radius = 1.0
- Height = 1.0
- The number of sectors = 36
- The number of stacks = 1
- Smoothness = true
- Up direction = 3 (X=1, Y=2, Z=3)
Apex Normal
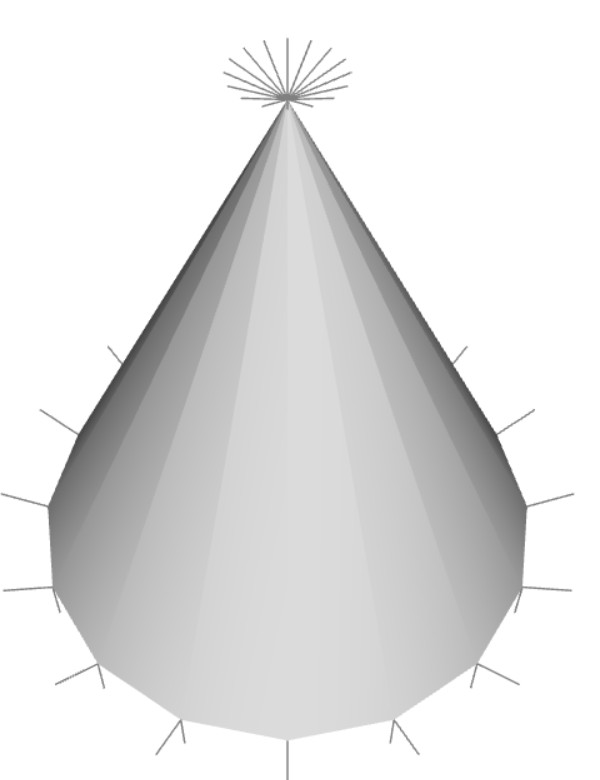
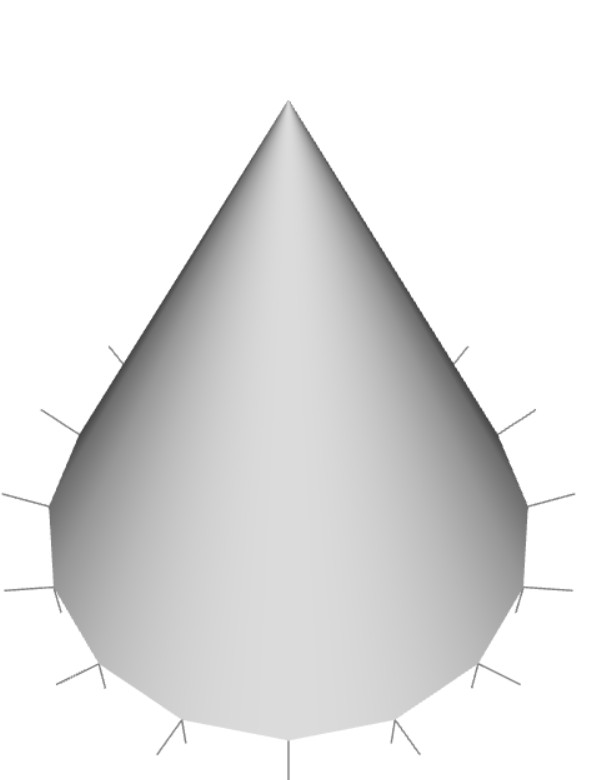
Edge lines are shown on the side of the cone because of multiple face normals at the apex.
Rendering a cone correctly with smooth shading is not easy because of the normal vector at the apex. The face normals of the side at the base are pointing outward radially, but they are merged to a single point, apex at the top. There are different multiple face normals at the apex, but there is only one vertex. It causes incorrect rendering, which is showing edge lines on the side even with per-fragment smooth shading. Adding more sides (sectors) cannot solve this problem.
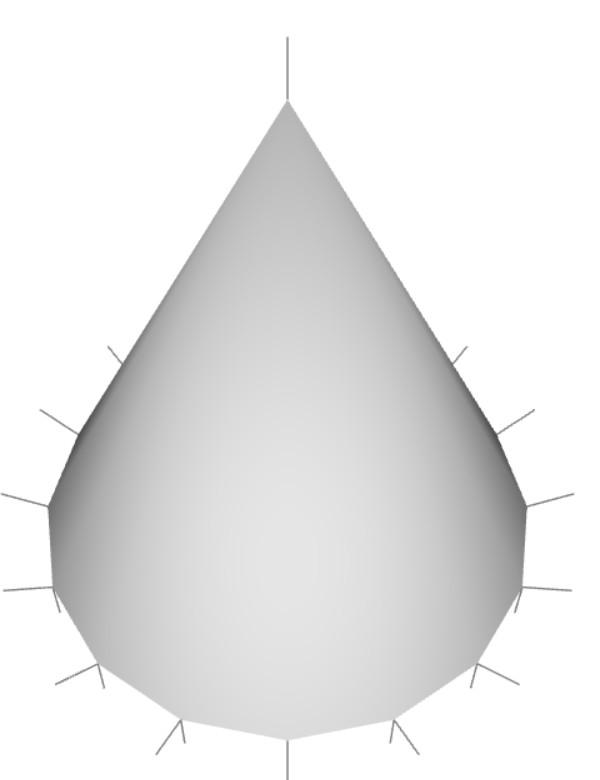
There are several approaches to avoid this visual artifact. The first method is averaging the normals at the apex to only one normal. Then, the normal at the apex becomes (0,0,1), which is pointing up direction of the cone. With ths method, the side of the cone looks smooth, however the apex point is now blunt (not sharp point anymore). You cannot tell where the apex is.
The second method is to set the apex normal to a zero-length vector (0,0,0) instead of (0,0,1). This method produces better rendering result than the first option. It significantly reduces the visual artifact around the side of the cone. And, the apex point is not blunt anymore, but it looks a black dot (not highlighted) due to the zero-length normal vector at the apex.
The third method is spliting the side of the cone multiple times by increasing the stack count. Because the side is divided by multiple stacks, the problematic section is only near the apex point, and the rest of the side are now rendering correctly. Also, the apex is now a sharp point. Not only fixing the rendering issue, but also it solves the texture distortion issue by increasing the number of stacks.
The following screenshots are comparing 3 different apex normal methods. Please see the live demo of drawing a cone by switching the apex normal vector modes.

Example: Drawing Cone

Download: cone.zip, coneShader.zip (Updated: 2024-07-25)
This example constructs cones with 36 sectors and 18 stacks, but with different shadings; flat, smooth or textured. With the default constructor (without arguments), it generates a cone with base radius = 1, height = 1, sectors = 36, and stacks = 1. By default, the apex is facing to +Z axis, but it can be changed by the last parameter of Cone class constructor (X=1, Y=2 or Z=3), or by calling setUpAxis() function after it is constructed. Press the space key to change the number of stacks of the cone. Pay attention that the visual artifacts at the center cone are reduced by increasing the stack count.
Cone.cpp class provides pre-defined drawing functions using OpenGL VertexArray; draw(), drawWithLines(), drawLines(), drawSide(), and drawBase().
// create a cone with base radius=1, height=2,
// sectors=3, stacks=4, smooth=true, up-axis=Z(3)
Cone cone(1, 2, 3, 4, true, 3);
// can change parameters later
cone.setBaseRadius(1.5f);
cone.setHeight(3.5f);
cone.setSectorCount(36);
cone.setStackCount(8);
cone.setSmooth(false);
cone.setUpAxis(2); // X=1, Y=2, Z=3
...
// draw cone using vertexarray
cone.draw(); // draw surface only
cone.drawWithLines(); // draw surface and lines
cone.drawSide(); // draw side only
cone.drawBase(); // draw botton only
This C++ class also provides getVertices(), getIndices(), getInterleavedVertices(), etc. in order to access the vertex data in GLSL. The following code draws a cone with interleaved vertex data using VBO, VAO and GLSL. Or, download coneShader.zip for more details.
// create a cone with default params;
// radius=1, height=1, sectors=36, stacks=1, smooth=true, up-axis=Z(3)
Cone cone;
// creat VAO to store VBO states
GLuint vaoId;
glGenVertexArrays(1, &vaoId1);
glBindVertexArray(vaoId1);
// copy interleaved vertex data (V/N/T) to VBO
GLuint vboId;
glGenBuffers(1, &vboId);
glBindBuffer(GL_ARRAY_BUFFER, vboId); // for vertex data
glBufferData(GL_ARRAY_BUFFER, // target
cone.getInterleavedVertexSize(), // data size, # of bytes
cone.getInterleavedVertices(), // ptr to vertex data
GL_STATIC_DRAW); // usage
// copy index data to VBO
GLuint iboId;
glGenBuffers(1, &iboId);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, iboId); // for index data
glBufferData(GL_ELEMENT_ARRAY_BUFFER, // target
cone.getIndexSize(), // data size, # of bytes
cone.getIndices(), // ptr to index data
GL_STATIC_DRAW); // usage
// enable vertex array attributes for bound VAO
glEnableVertexAttribArray(attribPos);
glEnableVertexAttribArray(attribNorm);
glEnableVertexAttribArray(attribTex);
// store vertex array pointers to bound VAO
int stride = cone.getInterleavedStride();
glVertexAttribPointer(attribPos, 3, GL_FLOAT, false, stride, 0);
glVertexAttribPointer(attribNorm, 3, GL_FLOAT, false, stride, (void*)(3*sizeof(float)));
glVertexAttribPointer(attribTex, 2, GL_FLOAT, false, stride, (void*)(6*sizeof(float)));
...
// bind VAO before drawing
glBindVertexArray(vaoId);
// draw a cone with VBO
glDrawElements(GL_TRIANGLES, // primitive type
cone.getIndexCount(), // # of indices
GL_UNSIGNED_INT, // data type
(void*)0); // offset to indices
// unbind VAO
glBindVertexArray(0);
Example: WebGL Cone with Normals (Interactive Demo)
It is a JavaScript implementation of Cone class, Cone.js, and rendering it with WebGL. Drag the slider of the stack count, or select different apex modes to see how the rendering of the cone is affected. The fullscreen version is also available Drawing Cone with Normals.
The following JavaScript code is to create and to render a cone object.
// create a cone with 6 params: baseR, height, sectors, stacks, smooth, up
let cone = new Cone(1, 2, 3, 4, false, 3);
...
// change params of cone later
cone.setBaseRadius(1);
cone.setHeight(3);
cone.setSectorCount(4);
cone.setStackCount(5);
cone.setSmooth(true);
...
// draw a cone with interleaved mode
gl.bindBuffer(gl.ARRAY_BUFFER, cone.vboVertex);
gl.vertexAttribPointer(gl.program.attribPosition, 3, gl.FLOAT, false, cone.stride, 0);
gl.vertexAttribPointer(gl.program.attribNormal, 3, gl.FLOAT, false, cone.stride, 12);
gl.vertexAttribPointer(gl.program.attribTexCoord0, 2, gl.FLOAT, false, cone.stride, 24);
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, cone.vboIndex);
gl.drawElements(gl.TRIANGLES, cone.getIndexCount(), gl.UNSIGNED_SHORT, 0);
...