OpenGL Normal Vector Transformation
Related Topics: OpenGL Transformation, OpenGL Matrix, Plane Equation
Overview
This page explains why transforming a normal vector from object space to eye space is;
When lighting is enabled in OpenGL, the normal vectors are used to determine how much light is received at the specified vertex or surface. This lighting processing is performed in the eye coordinate space, therefore, normal vectors in the object coordinates are also transformed to the eye coordinates with GL_MODELVIEW matrix.
However, normal vectors are transformed in a different way as vertices do. We cannot simply multiply GL_MODELVIEW matrix and normal vectors. Consider a normal vector (1,0,0) for a vertex (0,0,0). If GL_MODELVIEW matrix is simply translating 2 unit up along Y-axis, then the vertex coordinates will be (0,2,0). But, the normal vector should remain same as (1,0,0), not (1,2,0).
In order to understand how normal vectors are transformed to the eye space, think the normals as coefficients of plane equations, which are perpendicular to the plane.
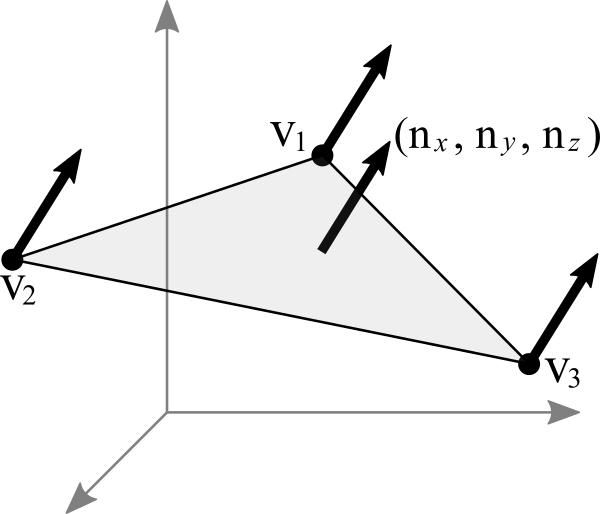
Imagine a triangular polygon with 3 vertices; v1-v2-v3, and the normal of this surface is 
as a homogeneous plane. (For Euclidean space, the normal is 
.) If we think of the triangle as a homogeneous plane, then the plane equation becomes;
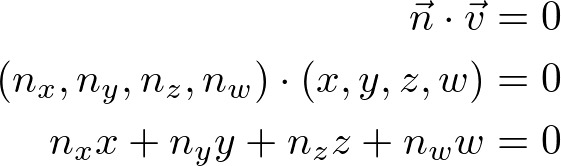
Since 3 vertices lie on this plane, the plane equation is also true when we substitute these vertices to the equation. For example, for 
, it satisfies;
The equivalent matrix form of the plane equation is;
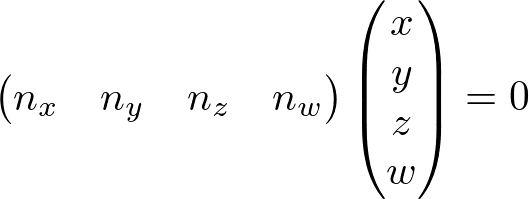
The plane equation is multiplying the transposed normal (nT) and the vertex (v) together. You can read "The vertex v in the object space lies on the plane with the normal 
".
Now, we modify the above equation to acquire the normal vector transformation formula by inserting GL_MODELVIEW matrix M-1M in between nT and v ;
(Note that the following equation is still equivalent to the above because of M-1M = I, identity matrix.)
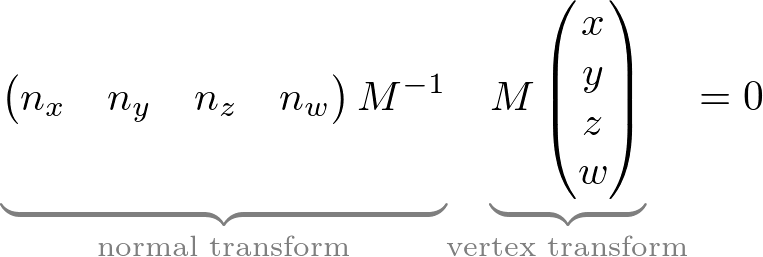
As you can see, the right part of the above equation 
is the vertex in the eye space because it is transformed by MODELVIEW matrix M, and the left part 
is going to be the normal vector in the eye space as well because this plane equation is also transformed.
It reads the above equation as "The transformed vertex lies on the transformed plane in the eye space with the transformed normal ".
Therefore, transforming a normal from the object space to the eye space with GL_MODELVIEW matrix M is;
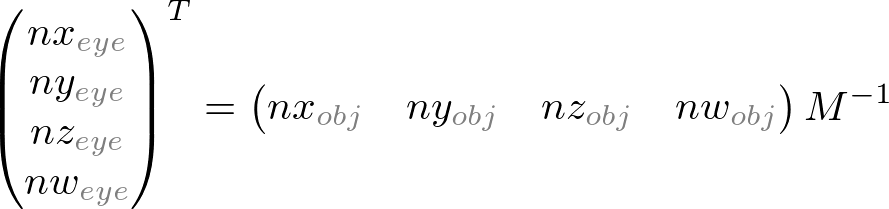
Or, by converting pre-multiplication to post-multiplication form, we get;
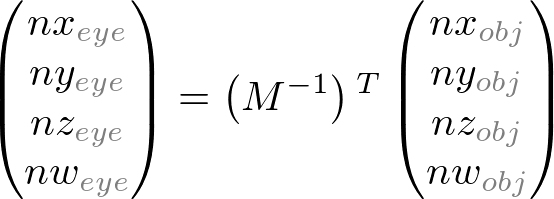
Case Study: Translation Only
Suppose a normal vector is (0, 0, 1) and the matrix has only translation part, moving to (2, 3, 4). The translation matrix, its inverse and transpose matrix 
and transformed normal would be;
, 
, 
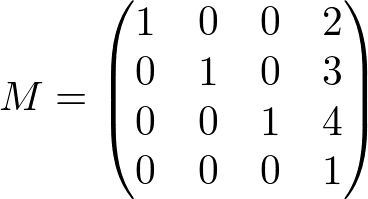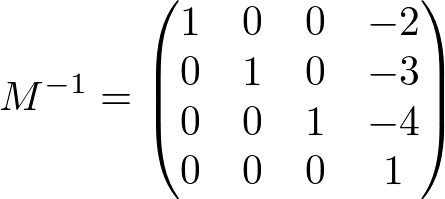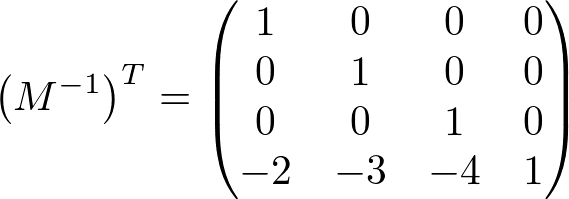
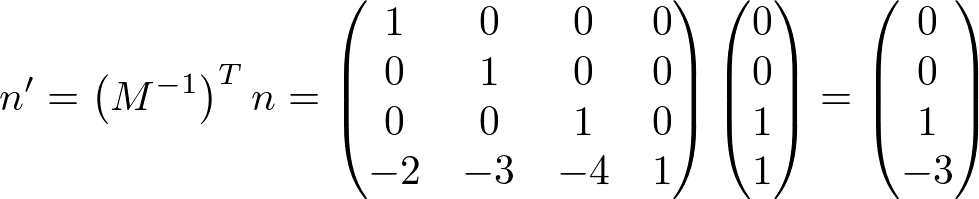
The normal vector remains unchanged (0, 0, 1) after translation. Therefore, it works as supposed to be if the matrix has translation only. Note that nw component is changed to -3, but it doesn't affect the direction and length of the normal vector.
Case Study: Rotation Only
If the transform matrix contains rotation only, the normal vectors are also rotated same as vertices do. The following is the matrix rotating 30 degree along X-axis, and transforming a normal vector (0, 0, 1) multiplying by the inverse and transpose matrix should become (0, -0.5, 0.866).
, 
, 
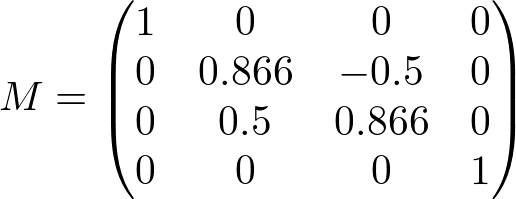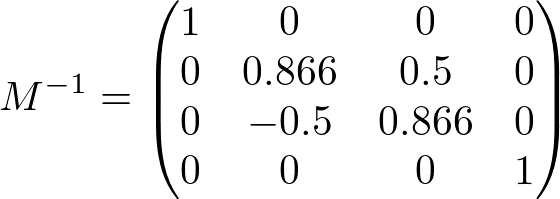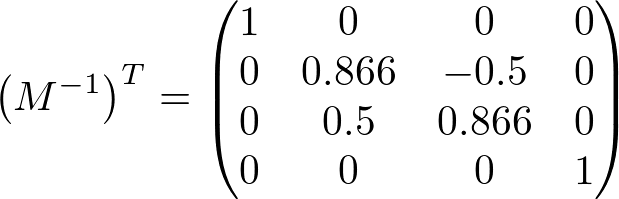
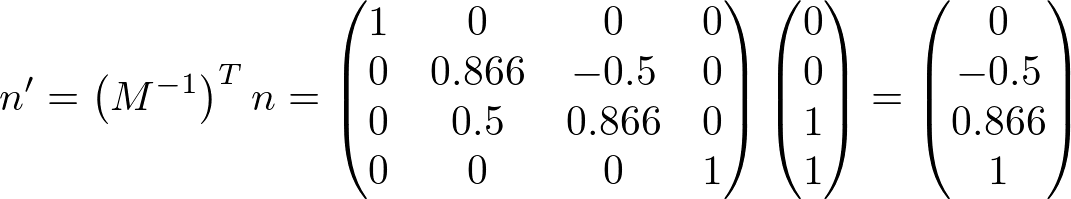
Note that the rotation-only matrix is unchanged after invert and transposed because it is an orthogonal matrix. (The inverse matrix is equal to the transpose matrix) Therefore, we don't need to compute the inverse and transpose process if the matrix has rotation only. We can multiply the matrix directly to the normal vectors.
Case Study: Scaling Only
Consider transforming a normal vector (0, 0.6, 0.8) by scaling (2, 4, 5). The transform matrix and the transformed normal with the inverse and transpose matrix follow;
, 
, 
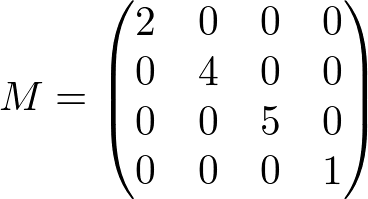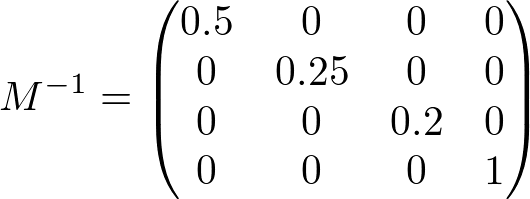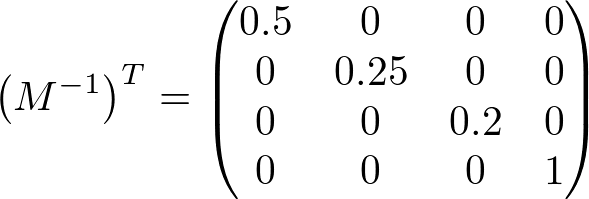
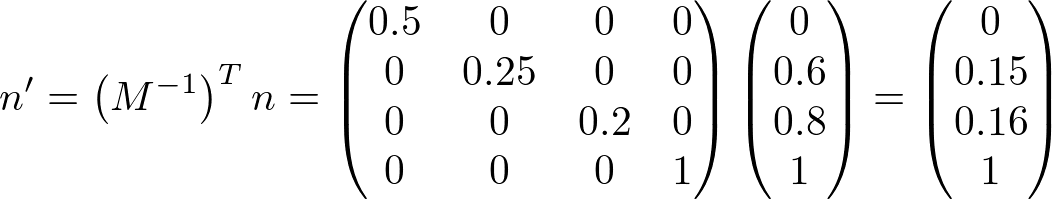
Note that the transformed normal vector is not unit length any more, plus its direction is also changed because of non-uniform scaling. Therefore, we need to re-normalize the normal vector in order to make it unit length.
What would be the result if the scale factor is -1, for example, scaling by (1, 1, -1)? See the visual result here.
Conclusion
Transforming a normal vector from the object space to the eye space multiplying by would work if the transform matrix contains translation and/or rotation. However, if the transform has scaling, then the normal vector must be re-normalized to make it unit length.
Since a rotation-only matrix is orthogonal (the inverse matrix and transpose matrix are same, so the original matrx and the inverse then transpose matrx are also identical), we can skip the process to invert and to transpose the matrix.
To optimize the performance of normal transformations, it would be better to define a separate matrix for the normal transformation, which is only containing the rotation parts from GL_MODELVIEW matrix (ignoring translation and scaling), and use this matrix to transform normal vectors from the object space to the eye space without computing inverse and transpose.
