Line Equation in 3D

Related Topics: Plane Equation
Download: StarGenerator.zip

• Line Equation
• Intersection of 2 Lines
• Example: Intersection of 2 Lines (Interactive Demo)
• Intersection of Line and Plane
• Example: Intersection of Line and Plane (Interactive Demo)
• Example: Star Generator
• Intersection of Line and Sphere

Line Equation

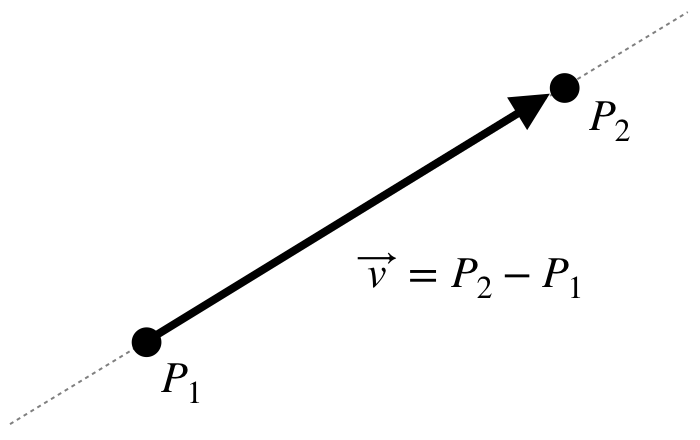
The equation of a line is defined with 2 known points. This page describes a line equation using parametric form; a point on the line and the direction vector of the line.

The direction vector can be computed by subtracting 2 known points;

Therefore, the parametric form of the line equation is;

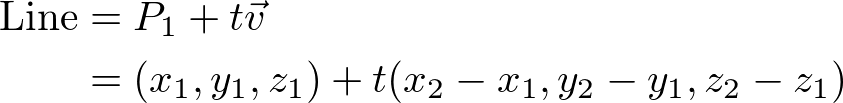
Or, each element (x, y, z) of the line can be written by the parameter t;

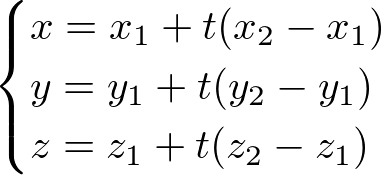
Notice that it is same as linear interpolation formula on each axis. If 0 < t < 1, it is an interpolation, otherwise extrapolation.

Also note that 2D line equation is frequently represented with slope-intercept form or standard form . However these forms are not suitable for computer algorithms because the slope of a vertical line is undefined (±∞), and plus the slope-itercept form cannot be used in 3D space.

Intersection of 2 Lines

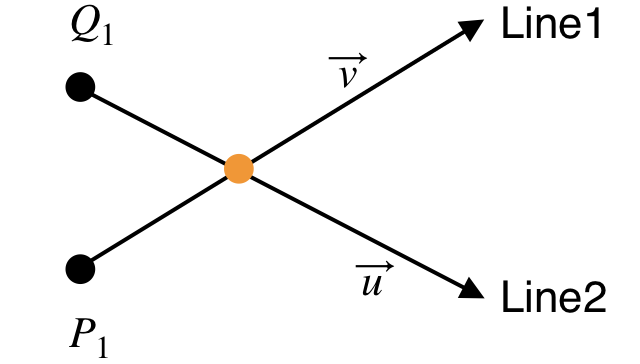
The intersection point of 2 lines is solving the linear system of 2 lines using vector algebra.

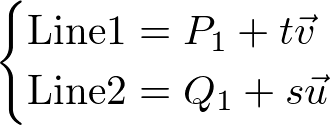
First, solve the linear system, Line1 = Line2 for t. Then substitute t into Line1 equation to find the intersection point (x, y, z).

(Reference: Intersection of two lines in three-space, Ronald Goldman, Graphics Gems, page 304, 1990)

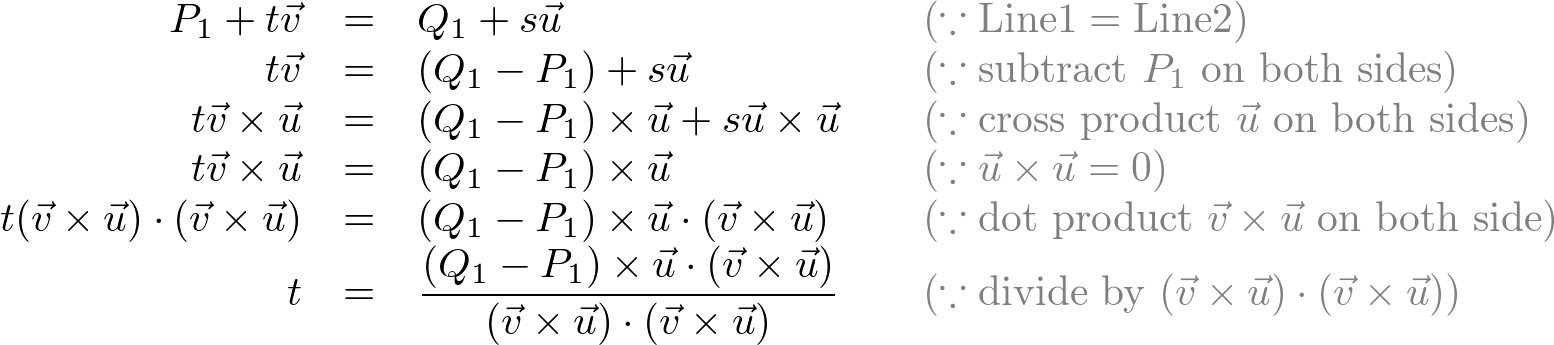
If two lines are parallel, the cross product of 2 direction vectors of the lines becomes zero. You can determine if two lines are intersect or not with;

Here is C++ code to find the intersection point of 2 lines. Please see the details in Line.cpp.

// dependency: Vector3, Line
struct Vector3
{
    float x;
    float y;
    float z;
};

class Line
{
    Vector3 direction;                 // (Vx, Vy, Vz)
    Vector3 point;                     // (Px, Py, Pz)
};


Vector3 intersect(Line& line1, Line& line2)
{
    Vector3 p = line1.point;           // P1
    Vector3 v = line1.direction;       // v
    Vector3 q = line2.point;           // Q1
    Vector3 u = line2.direction;       // u

    // find a = v x u
    Vector3 a = v.cross(u);            // cross product

    // find dot product = (v x u) . (v x u)
    float dot = a.dot(a);              // inner product

    // if v and u are parallel (v x u = 0), then no intersection, return NaN point
    if(dot == 0)
        return Vector3(NAN, NAN, NAN);

    // find b = (Q1-P1) x u
    Vector3 b = (q - p).cross(u);      // cross product

    // find t = (b.a)/(a.a) = ((Q1-P1) x u) .(v x u) / (v x u) . (v x u)
    float t = b.dot(a) / dot;

    // find intersection point by substituting t to the line1 eq
    Vector3 point = p + (t * v);
    return point;
}

Example: Intersection of 2 Lines in 2D (Interactive Demo)

The following JavaScript interactive demo is finding the intersection point from 2 lines in 2D. It requires WebGL enabled browsers.

Intersection of Line and Plane

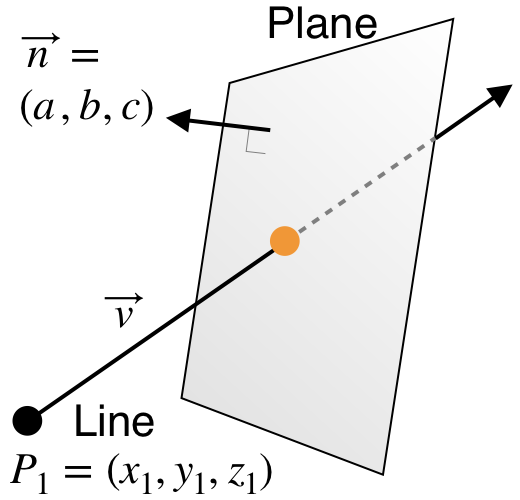
A plane equation in 3D is defined with its normal vector and a known point on the plane;

Please refer to Plane Equation to see how to derive the plane equation.

Finding the intersection point of a line and plane is solving a linear system of a line and plane.

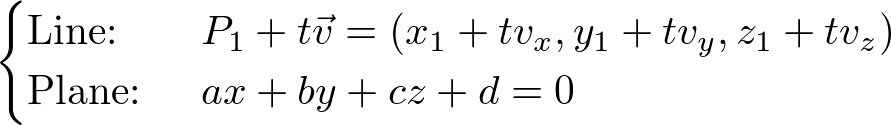
First, substitute of the plane equation with from the line equation. Then, solve for t;

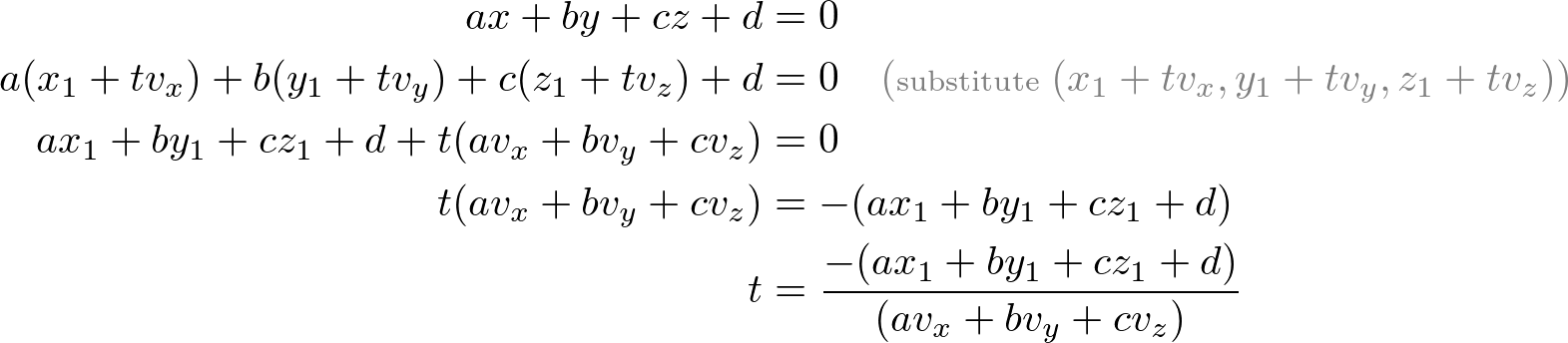
If the denominator part is zero, there is no intersection. And the sum of multiplications of the above equation can be replaced with dot products;

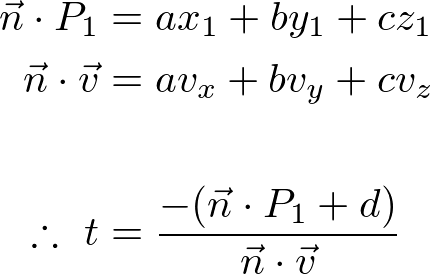
Here is C++ code to find the intersection point of a line and a plane.

// dependency: Vector3, Line, Plane
struct Vector3
{
    float x;
    float y;
    float z;
};

class Line
{
    Vector3 direction;                 // v
    Vector3 point;                     // p
};

class Plane
{
    Vector3 normal;                    // (a, b, c)
    Vector3 d;                         // constant term: d = -(a*x0 + b*y0 + c*z0)
};


Vector3 intersect(Line& line, Plane& plane)
{
    // from line = p + t * v
    Vector3 p = line.point;            // (x1, y1, z1)
    Vector3 v = line.direction;        // (Vx, Vy, Vz)

    // from plane: ax + by + cz + d = 0
    Vector3 n = plane.normal;          // (a, b, c)
    Vector3 d = plane.d;               // constant term of plane

    // dot products
    float dot1 = n.dot(v);             // a*Vx + b*Vy + c*Vz
    float dot2 = n.dot(p);             // a*x1 + b*y1 + c*z1

    // if denominator=0, no intersect
    if(dot1 == 0)
        return Vector3(NAN, NAN, NAN); // return NaN point

    // find t = -(a*x1 + b*y1 + c*z1 + d) / (a*Vx + b*Vy + c*Vz)
    float t = -(dot2 + d) / dot1;

    // find intersection point by substituting t to line eq
    return p + (t * v);
}

Example: Intersection of Line and Plane (Interactive Demo)

The following JavaScript interactive demo is finding the intersection point from a line and a plane in 3D. Use left and right mouse buttons to rotate the view, or to zoom in and out. It requires WebGL enabled browsers.

Example: Drawing N-point Star

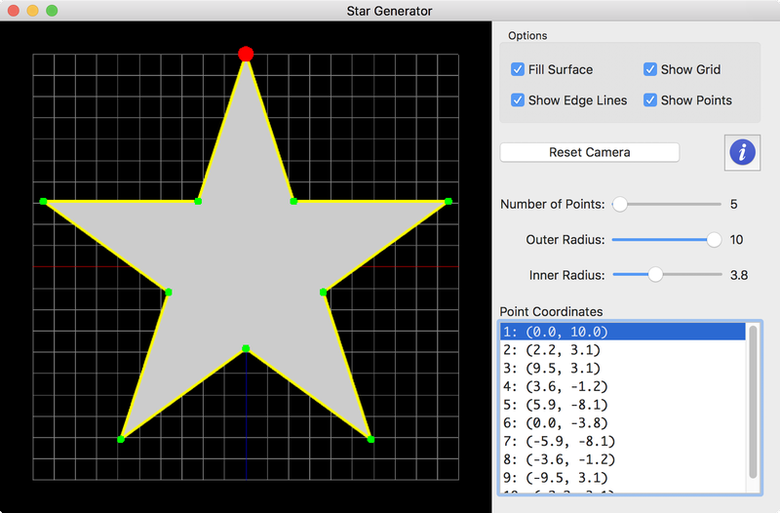
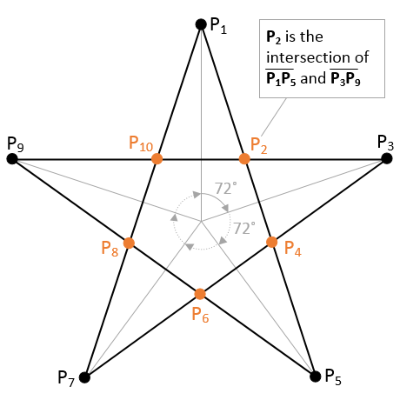
Download source and binary:
StarGenerator.zip (Updated: 2020-07-17)
StarGenerator_mac.zip (Updated: 2023-04-25)

Drawing a N-point star is a practical application using line intersection algorithm. The steps for drawing a star are;

Intersection of Line and Sphere

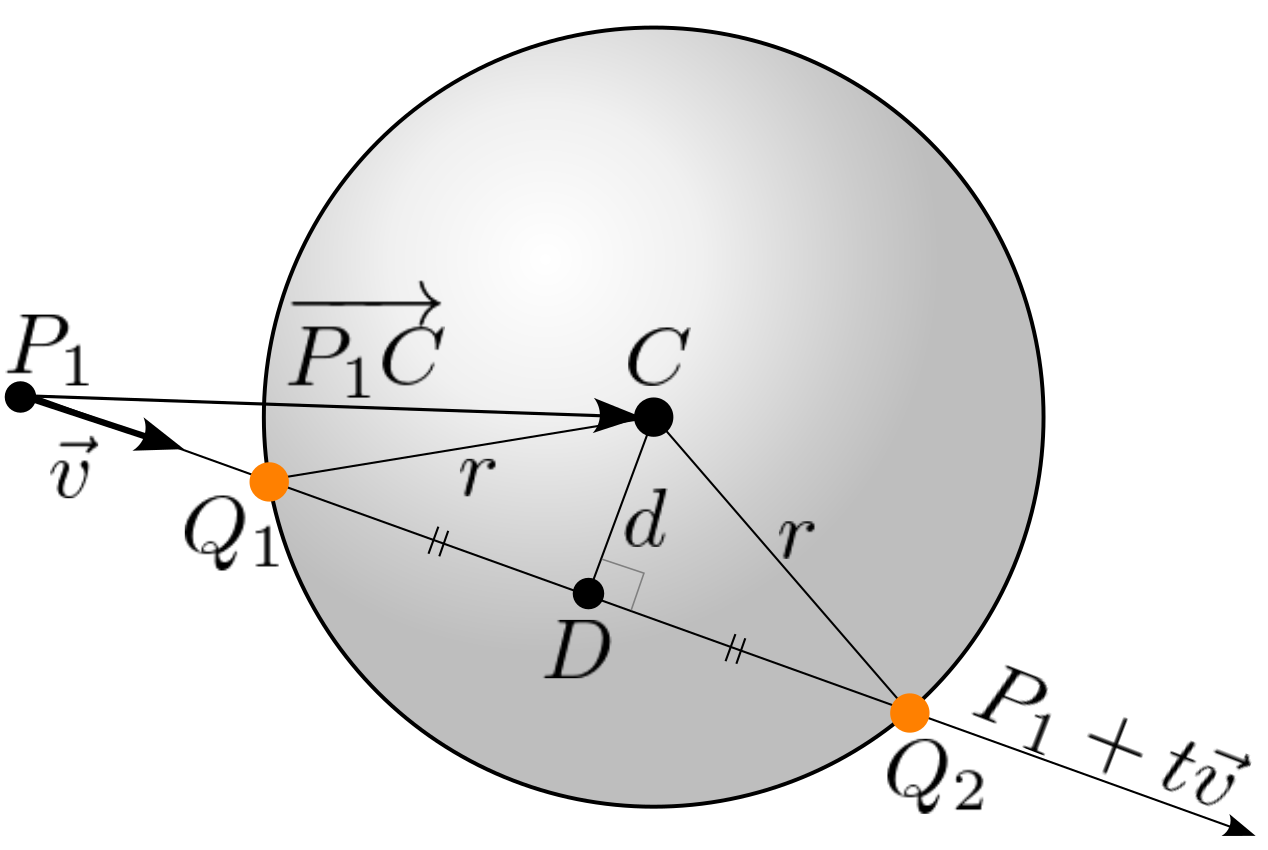
Finding the intersection point of a line and a sphere is very common in ray tracing algorithm because a sphere is the simplest geometry. One method is to substitute each x, y, z from the parametric line equation to the sphere equation and solve the quadratic equation for t.

The other method is using vector arithmetic. First, find the length between the starting point P₁ of the line equation and the point D on the line that is perpendicularly projected from the sphere center, C (See the diagram on the side).

It can be computed by projecting the vector from P₁ to the center of the sphere C onto the line, which is inner product of 2 vectors, and the direction vector of the line.

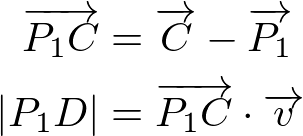
Then, find the length between Q₁ and D from 2 right-angle triangles C-D-P₁ and C-D-Q₁. It is actually the half distance between 2 intersection points Q₁ and Q₂.

Finally, we can find the intersection points, Q₁ and Q₂ by substituting and into the line equation for t.

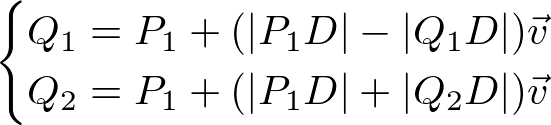
A line can intersect with a sphere in 3 ways. If the d is greater than the sphere radius, there is no intersection. If d is equal to r, then there is only 1 intersection point. If d is less than r, The line and sphere intersect with 2 points.

Here is C++ code to find the intersection points of a line and a sphere. It returns std::vector containing 0, 1 or 2 points. Please see the detail implementation in Line.cpp.

std::vector<Vector3> Line::intersect(Vector3& sphereCenter, float radius)
{
    std::vector<Vector3> points; // to store intersect points
    float r2 = radius * radius;

    // find perpendicular distance from sphere center to the line
    Vector3 pc = sphereCenter - point;
    float pd = pc.dot(direction);      // PC projected on the line
    float d2 = pc.dot(pc) - (pd * pd); // squared distance

    // if d > r, no intersection (do nothing)
    if(d2 <= r2)
    {
        const float EPSILON = 0.00001f;
        if(r2 - d2 < EPSILON)          // if d = r, only 1 intersect point
        {
            points.push_back(point + pd * direction);
        }
        else                           // if d < r, 2 intersect points
        {
            // find half distance between 2 points
            float dh = sqrt(r2 - d2);
            float t1 = pd - dh;        // t for Q1
            float t2 = pd + dh;        // t for Q2
            points.push_back(point + t1 * direction);
            points.push_back(point + t2 * direction);
        }
    }
    return points;
}