Plane Equation

Related Topics: Line Equation, Matrix
Download: plane.zip

• Distance from Origin
• Distance from a Point
• Intersection of 3 Planes
• Intersection of 2 Planes
• Intersection of Plane and Line
• Example: Intersection Line of 2 Planes (Interactive Demo)

Overview

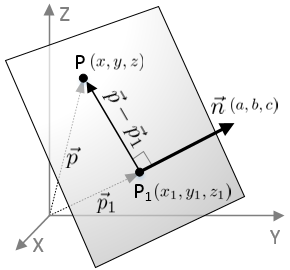
The equation of a plane in 3D space is defined with normal vector (perpendicular to the plane) and a known point on the plane.

Let the normal vector of a plane, and the known point on the plane, P₁. And, let any point on the plane as P.

We can define a vector connecting from P₁ to P, which is lying on the plane.

Since the vector and the normal vector are perpendicular each other, the dot product of two vector should be 0.

This dot product of the normal vector and a vector on the plane becomes the equation of the plane. By calculating the dot product, we get;

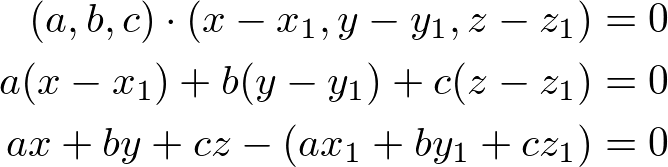
If we substitute the constant terms to , then the plane equation becomes simpler;

Distance from Origin

If the normal vector is normalized (unit length), then the constant term of the plane equation, d becomes the distance from the origin.

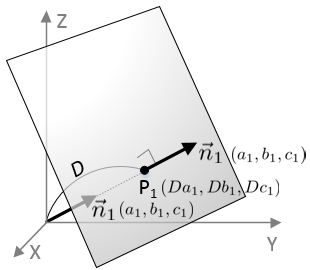
If the unit normal vector (a₁, b₁, c₁), then, the point P₁ on the plane becomes (Da₁, Db₁, Dc₁), where D is the distance from the origin. The equation of the plane can be rewritten with the unit vector and the point on the plane in order to show the distance D is the constant term of the equation;

    

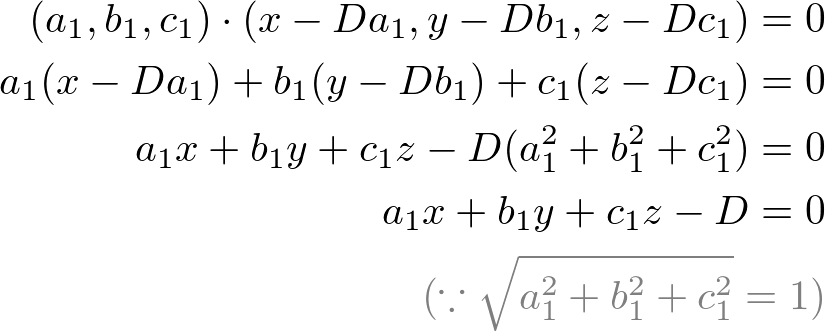
Therefore, we can find the distance from the origin by dividing the standard plane equation by the length (norm) of the normal vector (normalizing the plane equation). For example, the distance from the origin for the following plane equation with normal (1, 2, 2) is 2;

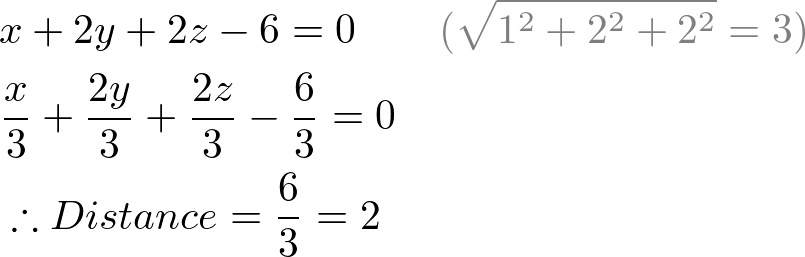
Distance from a Point

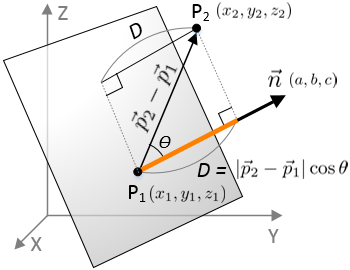
The shortest distance from an arbitrary point P₂ to a plane can be calculated by the dot product of two vectors and , projecting the vector to the normal vector of the plane.

The distance D between a plane and a point P₂ becomes;
  

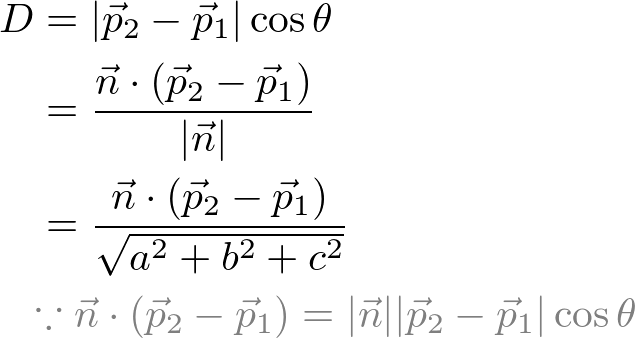
The numerator part of the above equation, is expanded;

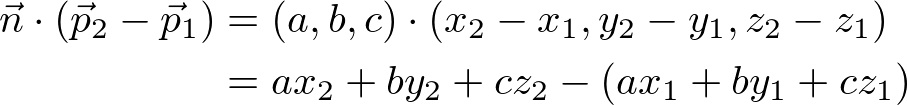
Finally, we put it to the previous equation to complete the distance formula;

Note that the distance formula looks like inserting P₂ into the plane equation, then dividing by the length of the normal vector. For example, the distance from a point (-1, -2, -3) to a plane x + 2y + 2z - 6 = 0 is;

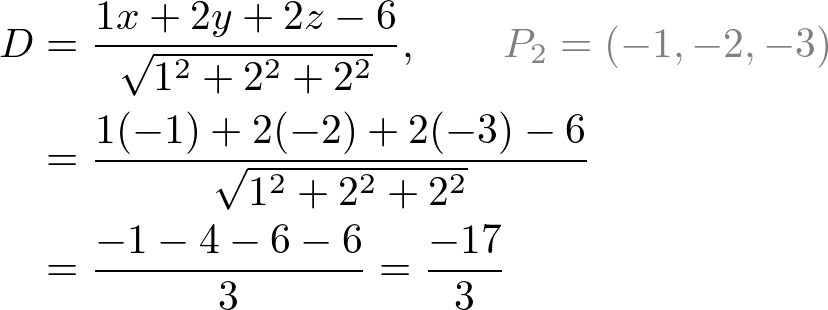
Notice this distance is signed; can be negative value. It is useful to determine the direction of the point. For example, if the distance is positive, the point is in the same side where the normal is pointing to. And, a negative distance means the point is in opposite side.

Intersection of 3 Planes

Before finding the intersection of 2 planes, we discuss finding the intersection of 3 planes first. This formular will be used for 2-plane intersection.

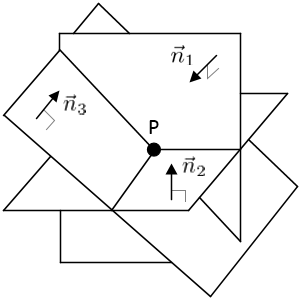
There are various ways to intersect 3 planes, but we will look into only special case; intersecting 3 planes at a point. In order to find the intersection point P (x, y, z), we solve the linear system of 3 planes.

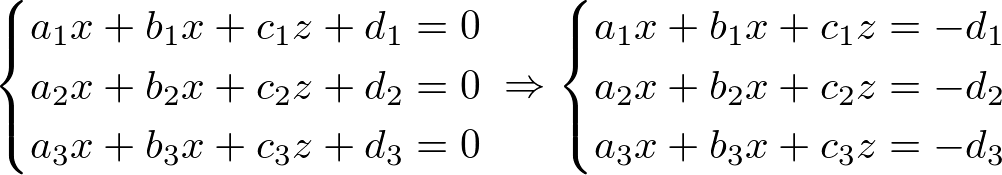
Or, in matrix form;

Therefore, solving the linear system is finding the inverse matrix.

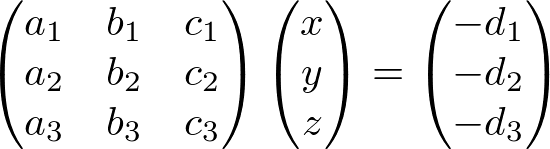
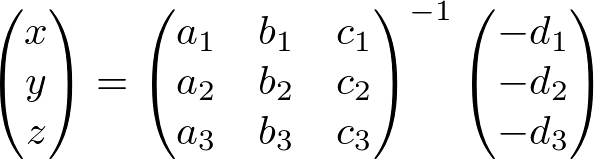
Let the 3x3 matrix A, and the intesection point is computed by Cramer's rule;


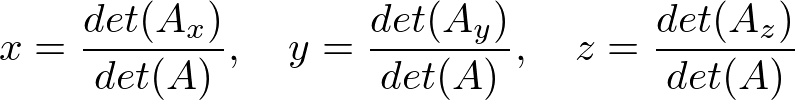
where the determinants are;

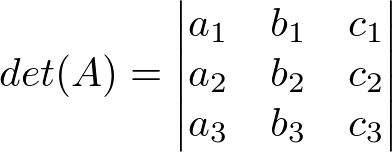
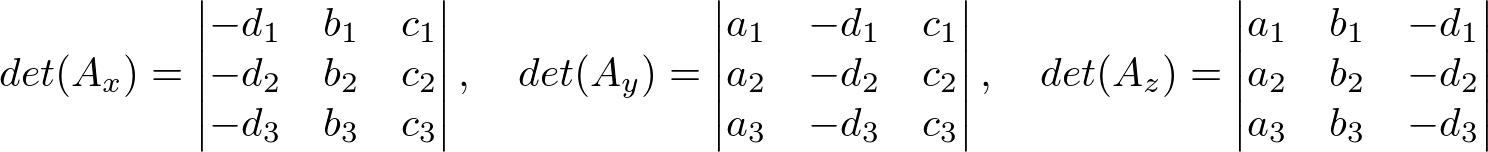
Let's calculate first.

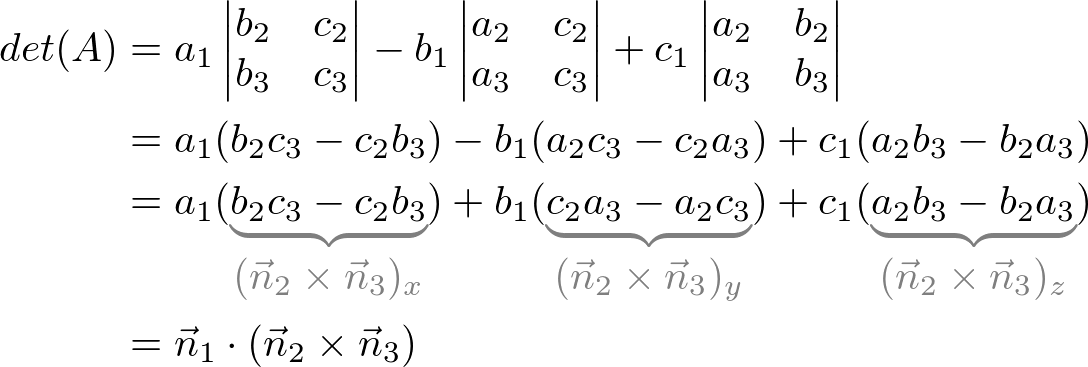
Notice that the determinant can be expressed as vector notation (cross product and inner product) to simplify the equation. In order to intersect at a point (having only 1 solution), the determinant must be not zero;

In a similar way, other determintants can be found;

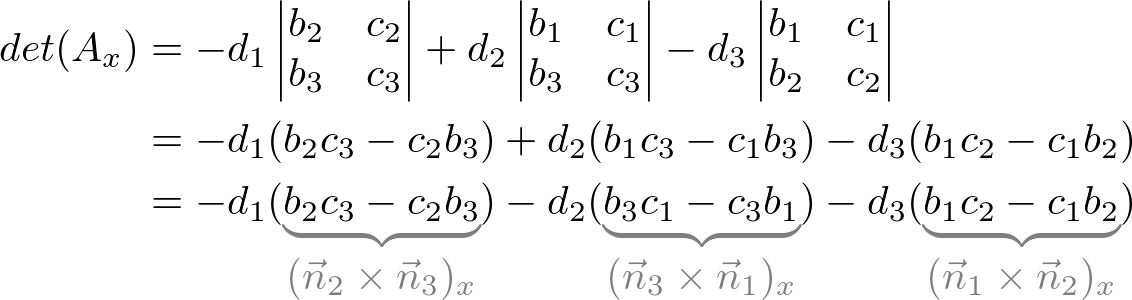
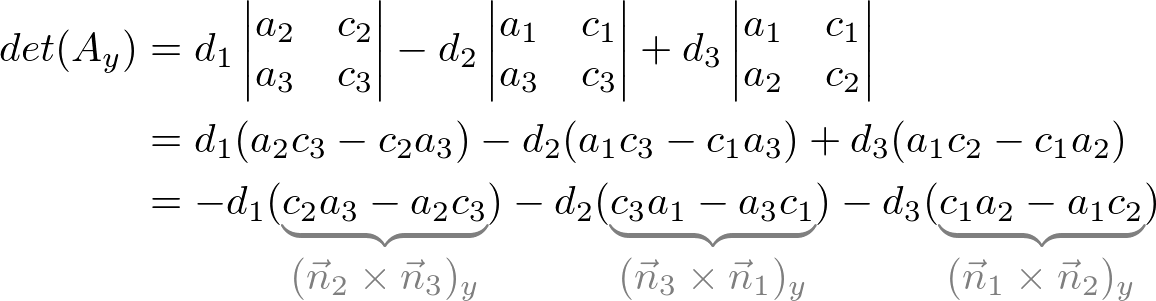
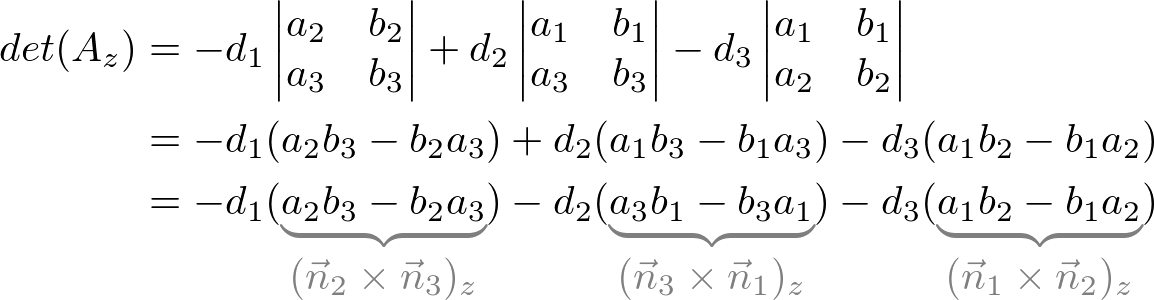
Therefore, the intersection of the point, P (x, y, z) is;

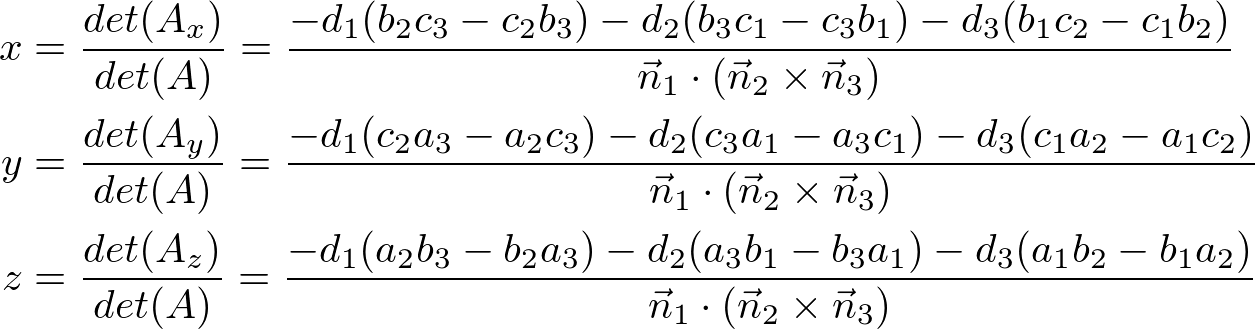
And, P (x, y, z) can be written in matrix form;

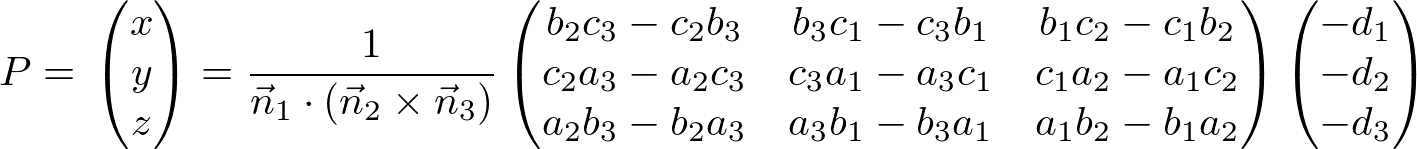
Or, it can be expressed in simpler vector form as well;

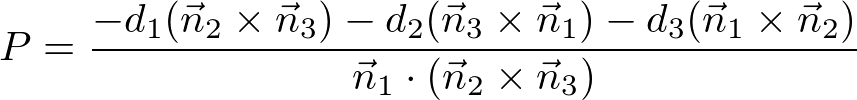
Intersection of 2 Planes

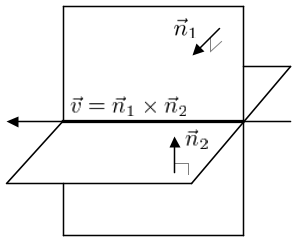
When 2 planes are intersected, it produces a line. A line equation can be expressed with its direction vector and a point on the line;

The direction vector of the line is perpendicular to both normal vectors and , so it is cross product of them;

Now, find any point on the line using the formula in the previous section for the intersection of 3 planes by adding a third plane. We can pick the simplest plane, which the normal of the plane is and it passes through the origin, . Therefore, the third plane equation becomes or .

Then, solve the linear system of 3 planes using the above formula;

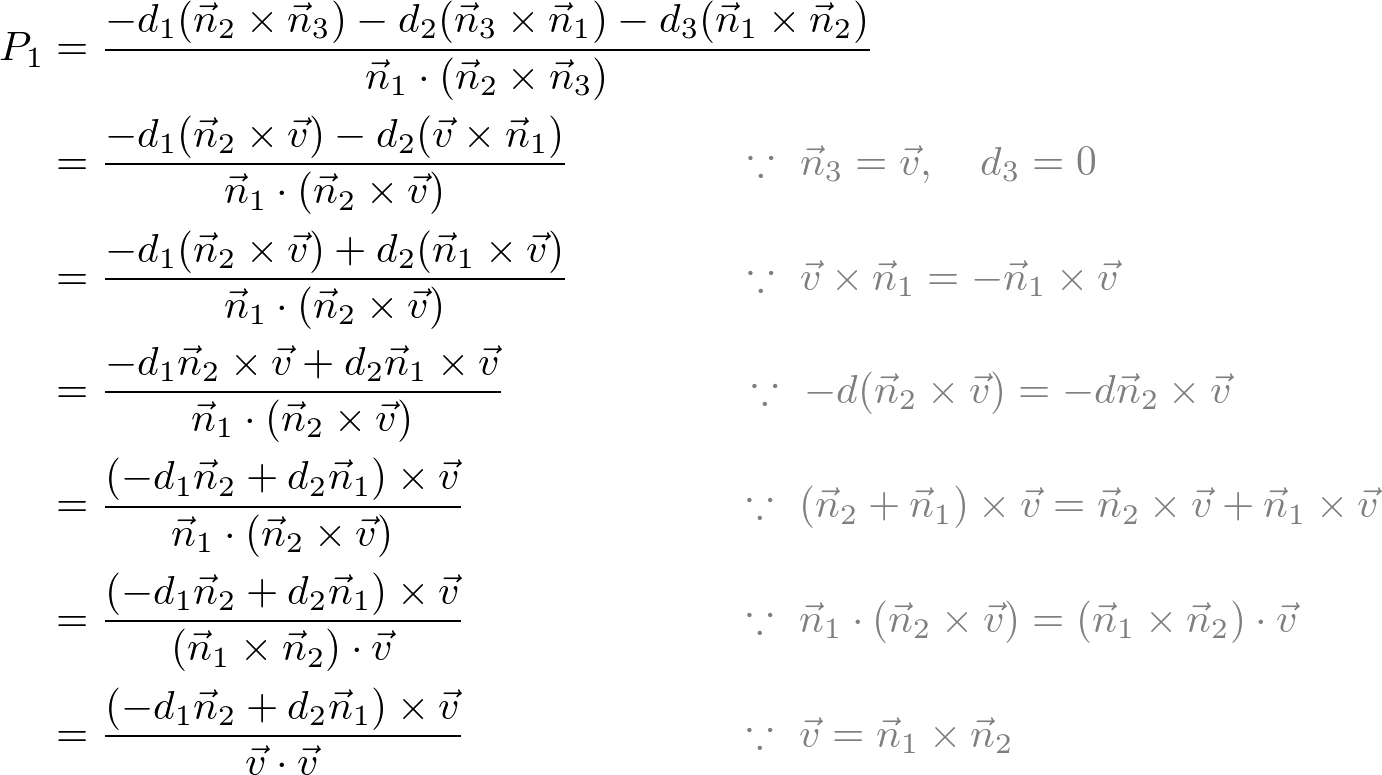
Once the point on the line is found, we can finally construct the line equation as; .

Here is C++ implementation to find the intersection line of 2 planes. Please see Plane.cpp for more detail.

// dependency: Vector3, Line, Plane
struct Vector3
{
    float x;
    float y;
    float z;
};

class Line
{
    Vector3 direction;                 // v
    Vector3 point;                     // p
};

class Plane
{
    Vector3 normal;                    // (a, b, c)
    Vector3 d;                         // constant term: d = -(a*x0 + b*y0 + c*z0)
};


Line intersect(Plane& plane1, Plane& plane2)
{
    Vector3 n1 = plane1.normal;
    Vector3 n2 = plane2.normal;
    float d1 = plane1.d;
    float d2 = plane2.d;

    // find direction vector of the intersection line
    Vector3 v = n1.cross(n2);                   // cross product

    // if |direction| = 0, 2 planes are parallel (no intersect)
    // return a line with NaN
    if(v.x == 0 && v.y == 0 && v.z == 0)
        return Line(Vector3(NAN, NAN, NAN), Vector3(NAN, NAN, NAN));

    // find a point on the line, which is also on both planes
    // choose simplest plane where d=0: ax + by + cz = 0
    float dot = v.dot(v);                       // V dot V
    Vector3 u1 =  d2 * n1;                      // d2 * N1
    Vector3 u2 = -d1 * n2;                      //-d1 * N2
    Vector3 p = (u1 + u2).cross(v) / dot;       // (d2*N1-d1*N2) X V / V dot V

    return Line(v, p);
}

Intersection of Plane and Line

A plane and a line can meet at a point. The point of intersection is solving a linear system of a plane and a line;

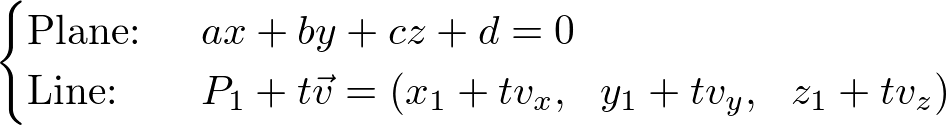
Solving the linear system for t;

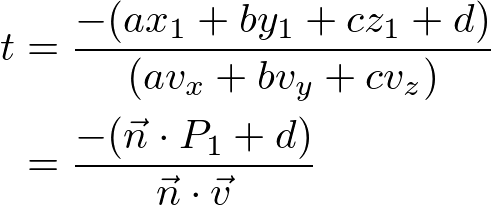
Check the detail explanation of how to derive the solution in the line equation page. It also provides C++ code snippet and an interactive demo.

Example: Intersection line of 2 Planes (Interactive Demo)

The following interactive demo is finding the intersection line from 2 planes in 3D. Use left mouse button to rotate the view, and right button to zoom in and out. It requires WebGL enabled browsers.

You can download C++ version plane.zip.