MacLaurin series of Exponential function,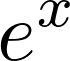 
The MacLaulin series (Taylor series at 
) representation of a function .png){kind=small}
is
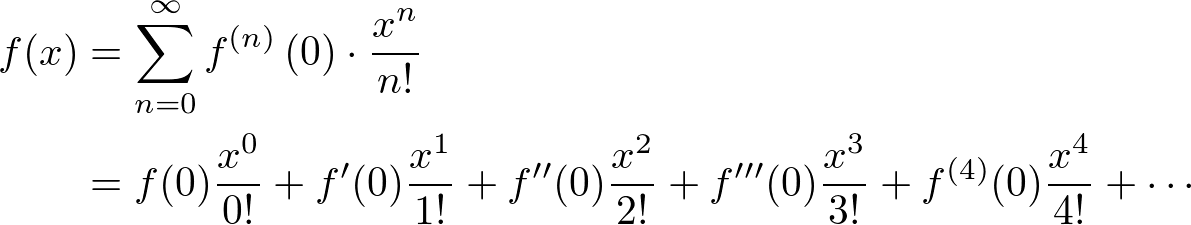
The derivatives of the exponential function 
and their values at are:
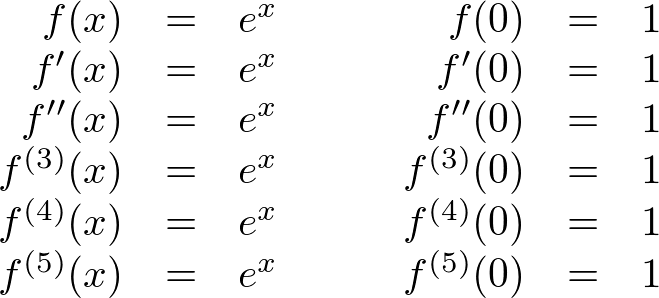
Note that the derivative of is also and 
. We substitute this value of 
in the above MacLaurin series:
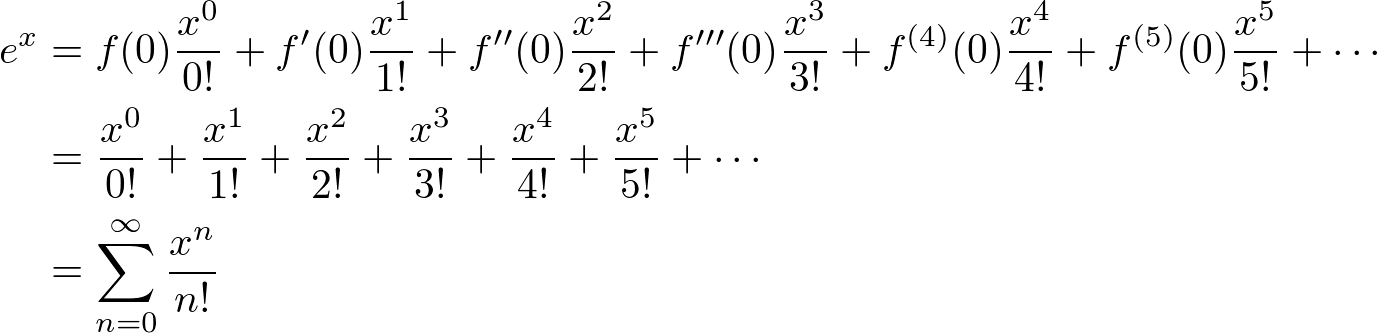
We can also get the MacLaurin series of 
by replacing 
to 
:
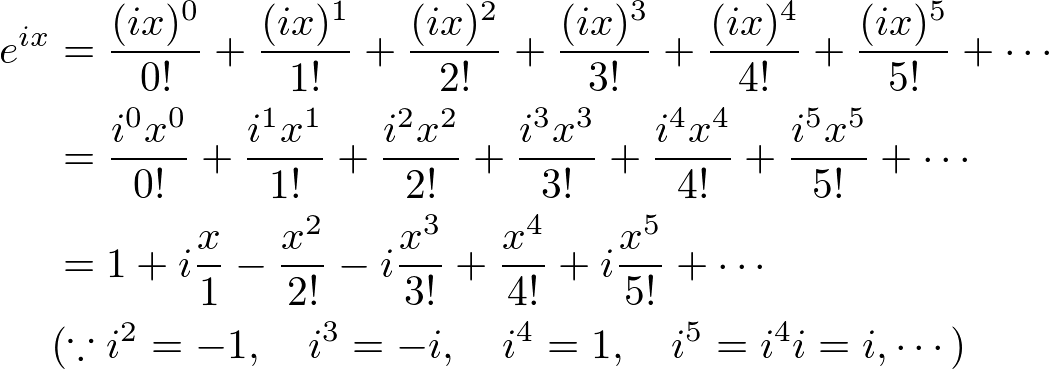
is used in Euler's Equation.
