Euler's Equation
Related Topics: Quaternion
![]()
Euler's equation is one of most remarkable and mysterious discoveries in Mathematics. Euler's equation (formula) shows a deep relationship between the trigonometric function and complex exponential function.
- Discovery of Euler's Equation
- Graph of Euler'sEquation
- Meaning of Euler's Equation
- 2D Rotation with Euler's Equation
- Euler Identity
- Proof of Euler's Equation
Discovery of Euler's Equation
First, take a look the Taylor series representation of exponential function, ![]() and trigonometric functions, sine,
and trigonometric functions, sine, ![]() and cosine,
and cosine, ![]() .
.
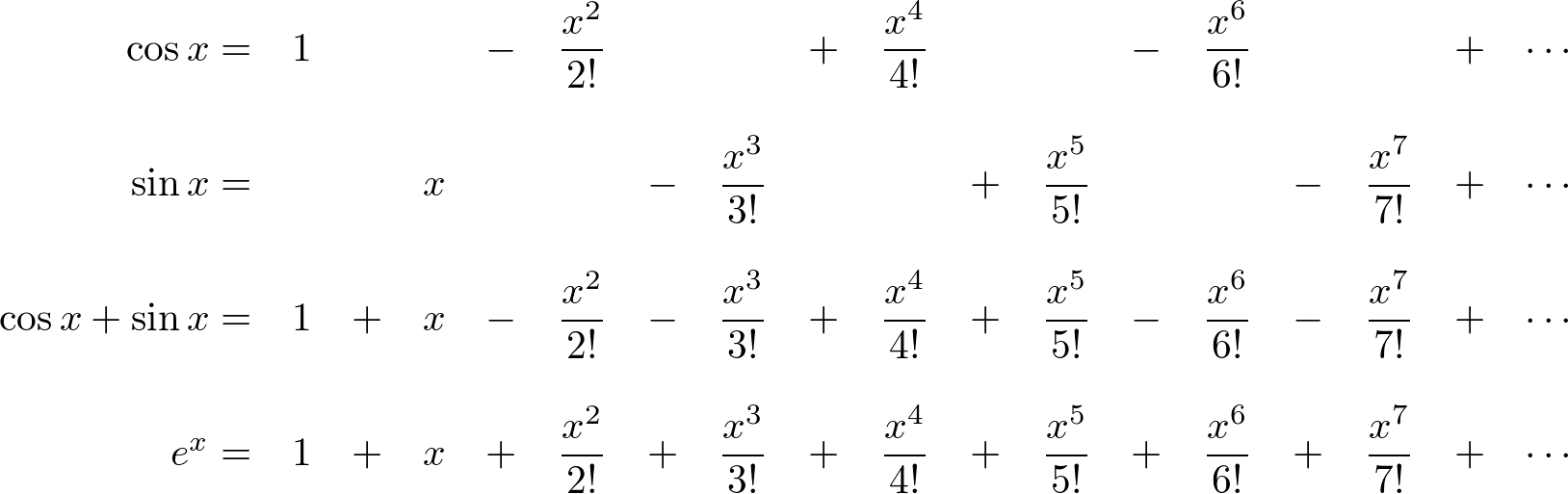
Let's compare ![]() with
with ![]() . Notice
. Notice ![]() is almost identical to Taylor series of
is almost identical to Taylor series of ![]() ; all terms in the series are exactly same except signs. As you know, the exponential function,
; all terms in the series are exactly same except signs. As you know, the exponential function, ![]() increases exponentially as input x grows. But, what does this exponential function have to do with periodic (oscillating) functions,
increases exponentially as input x grows. But, what does this exponential function have to do with periodic (oscillating) functions, ![]() and
and ![]() ?
?
Mathematicians had tried to figure out this weird relationship between the exponential function and the sum of 2 oscillating functions. Finally, Leonhard Euler completed this relation by bringing the imaginary number, ![]() into the above Taylor series;
into the above Taylor series; ![]() instead of
instead of ![]() and
and ![]() instead of
instead of ![]() .
.
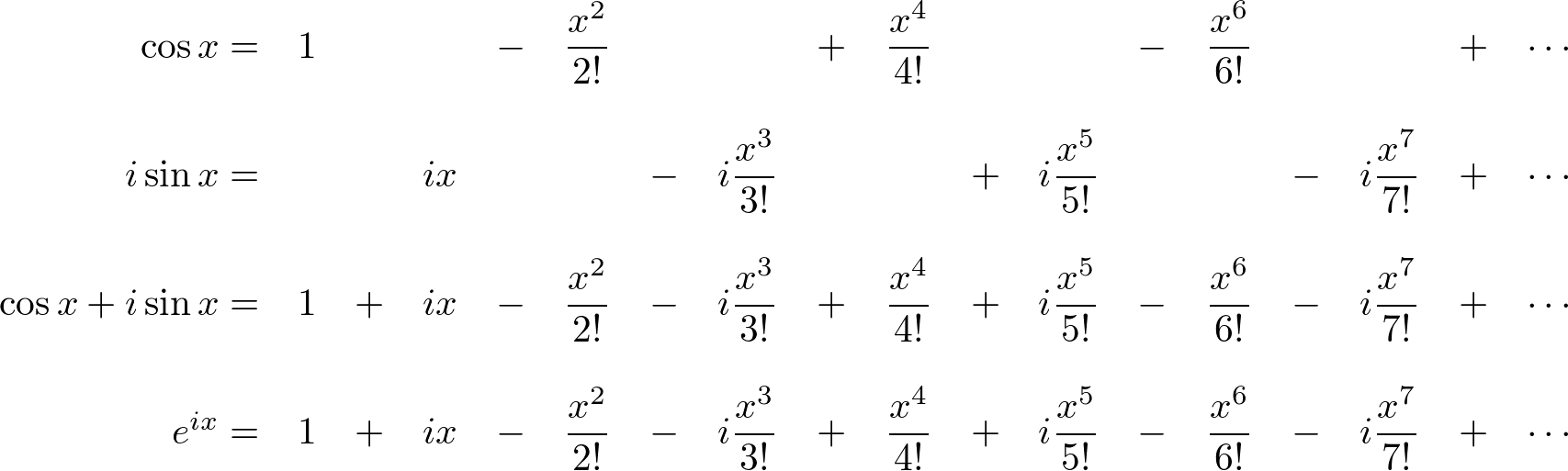
Now, we find out ![]() equals to
equals to ![]() , which is known as Euler's Equation.
, which is known as Euler's Equation.
Graph of Euler's Equation
We know that the exponential function, ![]() is increasing exponentially as x grows. But, what does the function
is increasing exponentially as x grows. But, what does the function ![]() look like?
look like?
The following images show the graph of the complex exponential function, ![]() , by plotting the Taylor series of
, by plotting the Taylor series of ![]() in the 3D complex space (x - real - imaginary axis). Surprisingly, it is a spiral spring (coil) shape, rotating around a unit circle. And, when it is projected to the real number (top view) and imaginary number axis (side view), it becomes a trigonometric function, respectively cosine and sine.
in the 3D complex space (x - real - imaginary axis). Surprisingly, it is a spiral spring (coil) shape, rotating around a unit circle. And, when it is projected to the real number (top view) and imaginary number axis (side view), it becomes a trigonometric function, respectively cosine and sine.
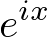
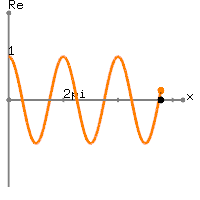
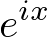
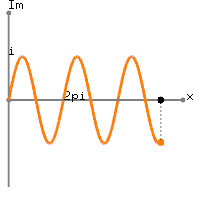
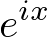
This graphical representation of the complex exponential function, ![]() clearly shows the relation to the trigonometric function; the real number part of
clearly shows the relation to the trigonometric function; the real number part of ![]() is cosine and the imaginary part of
is cosine and the imaginary part of ![]() is sine function with the period of
is sine function with the period of ![]() in radians.
in radians.
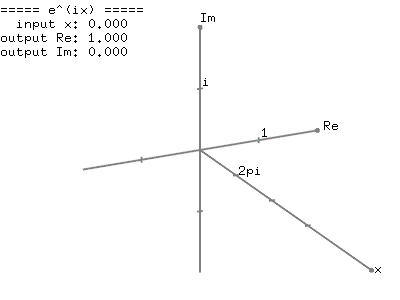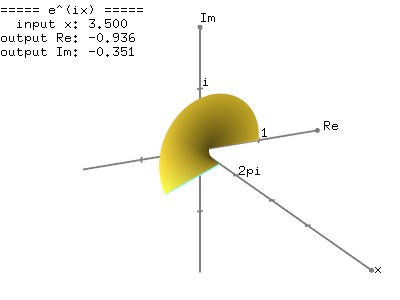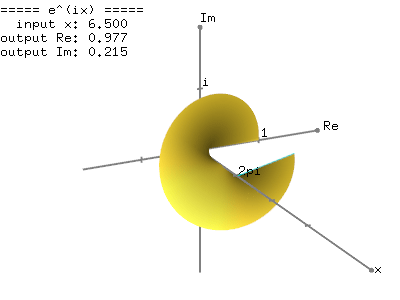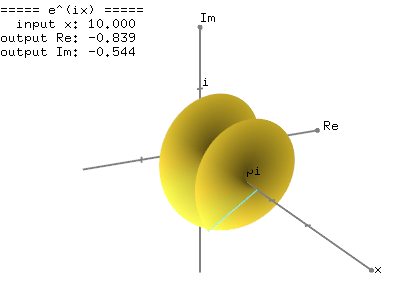
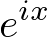
This is an interactive OpenGL application to draw the complex exponential function, ![]() in 3D.
in 3D.
You can download the source codes and binary:
euler.zip (Updated 2021-04-08)
Use the mouse cursor to rotate the view and use 'd' key to change drawing modes.
Meaning of Euler's Equation
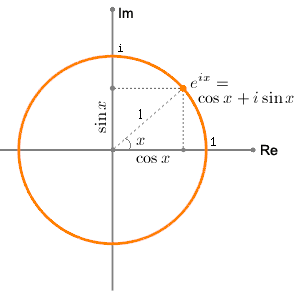
 on the complex plane
on the complex plane
When the graph of ![]() is projected to the complex plane, the function
is projected to the complex plane, the function ![]() is tracing on the unit circle. It is a periodic function with the period
is tracing on the unit circle. It is a periodic function with the period ![]() .
.
It means that raising ![]() to an imaginary power
to an imaginary power ![]() produces the complex number with the angle x in radians. This polar form of
produces the complex number with the angle x in radians. This polar form of ![]() is very convenient to represent rotating objects or periodic signals because it can represent a point in the complex plane with only single term instead of two terms,
is very convenient to represent rotating objects or periodic signals because it can represent a point in the complex plane with only single term instead of two terms, ![]() . Plus, it simplifies the mathematics when used in multiplication, for example,
. Plus, it simplifies the mathematics when used in multiplication, for example, ![]() .
.
The complex exponential forms are frequently used in electrical engineering and physics. For example, a periodic signal can be represented the sum of sine and cosine functions in Fourier analysis, and the movement of a mass attached to a string is also sinusodial. These sinusodial functions can be replaced with the complex exponential forms for simpler computation.
We can extend this polar form representation for any complex number.
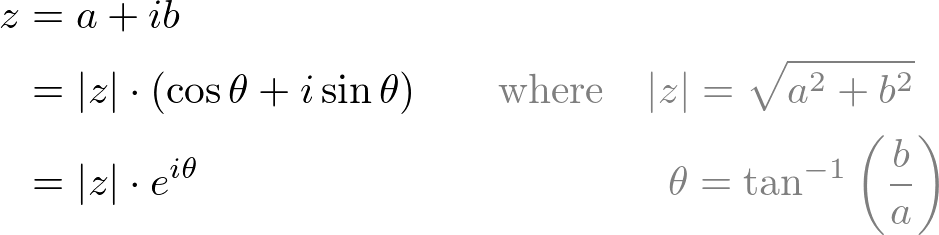
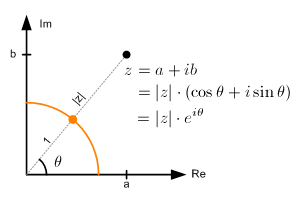
The magnitude (norm), |z| of the complex number is a scalar value and can be rewrtten by using the laws of exponent and logarithm:
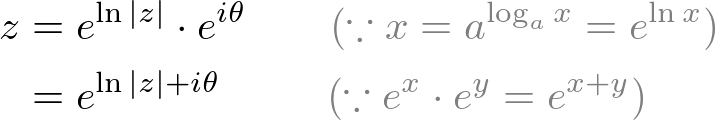
2D Rotation with Euler's Equation
The multiplication of two complex numbers implies a rotation in 2D space.
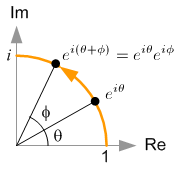
Take a look at the following figure showing 2 complex numbers on the unit circle of the complex plane.
When we compare these two complex numbers, we notice that the sum of angles in the imaginary exponential form equals to the product of two complex numbers, ![]() . It tells us multiplying
. It tells us multiplying ![]() by
by ![]() performs rotating
performs rotating ![]() with angle
with angle ![]() .
.
We can extend it to any arbitary complex number. In order to rotate a complex number z = x + iy with a certain angle ![]() , we simply multiply
, we simply multiply ![]() to the number. Then, the rotated result z' becomes
to the number. Then, the rotated result z' becomes ![]() .
.
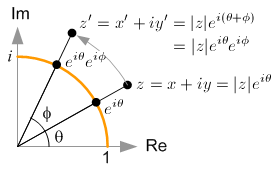
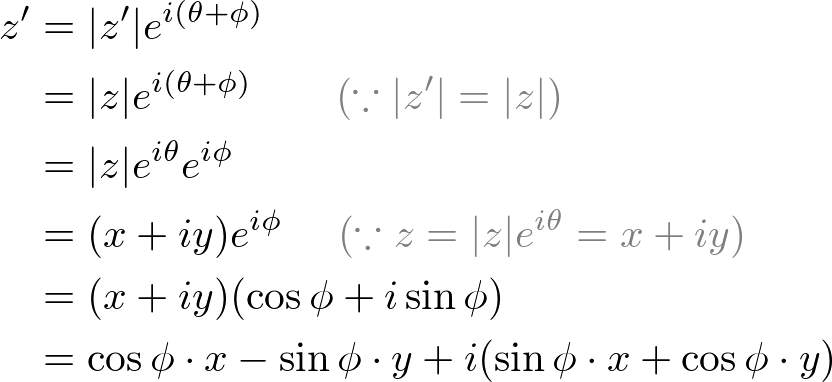
If we re-write it as a matrix form by omitting ![]() , it becomes a 2x2 rotation matrix that we are familiar with.
, it becomes a 2x2 rotation matrix that we are familiar with.
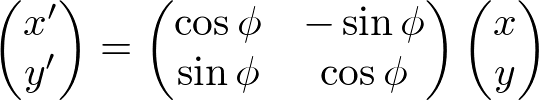
It can be extended for 3D rotation by multiplying quaternion instead. Note that quaternion has a rotation axis vector u, instead of a complex number i.
![]()
Euler Identity
If we substitute the value ![]() into Euler's equation, then we get:
into Euler's equation, then we get:
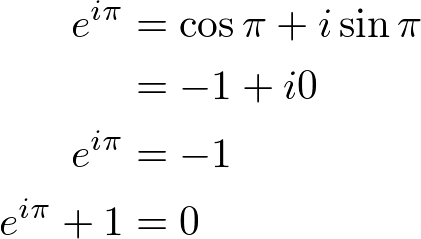
This equation is called Euler Identity showing the link between 5 fundamental mathematical constants; 0, 1, ![]() ,
, ![]() , and
, and ![]() .
.
Logarithmic function is only defined for the domain x > 0. But, Euler Identity allows to define the logarithm of negative x by converting exponent to logarithm form:
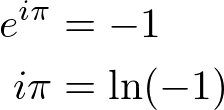
If we substitute ![]() to Euler's equation, then we get:
to Euler's equation, then we get:
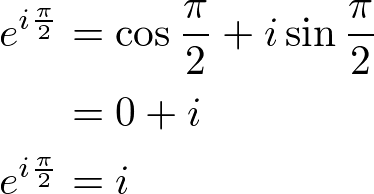
Then, raise both sides to the power ![]() :
:
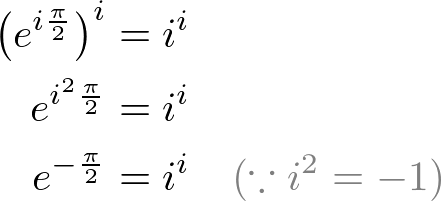
The above equation tells us that ![]() is actually a real number (not an imaginary number).
is actually a real number (not an imaginary number).
Proof of Euler's Equation
This is a proof using calculus. Let's start with the right-hand side only and its differentiate is:
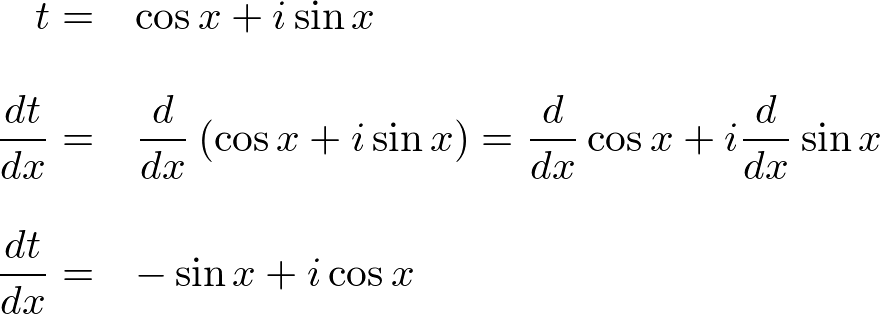
Modify the right-hand side of the above equation:
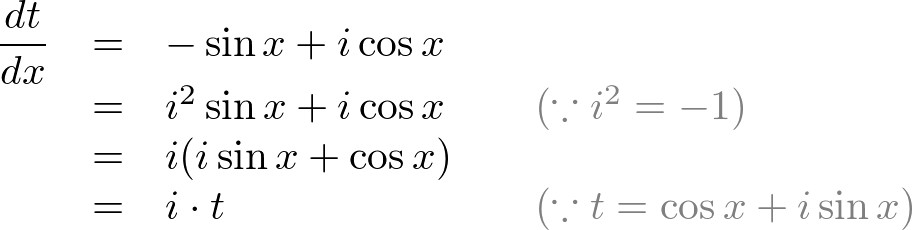
Move t to left-hand side, then apply integral:
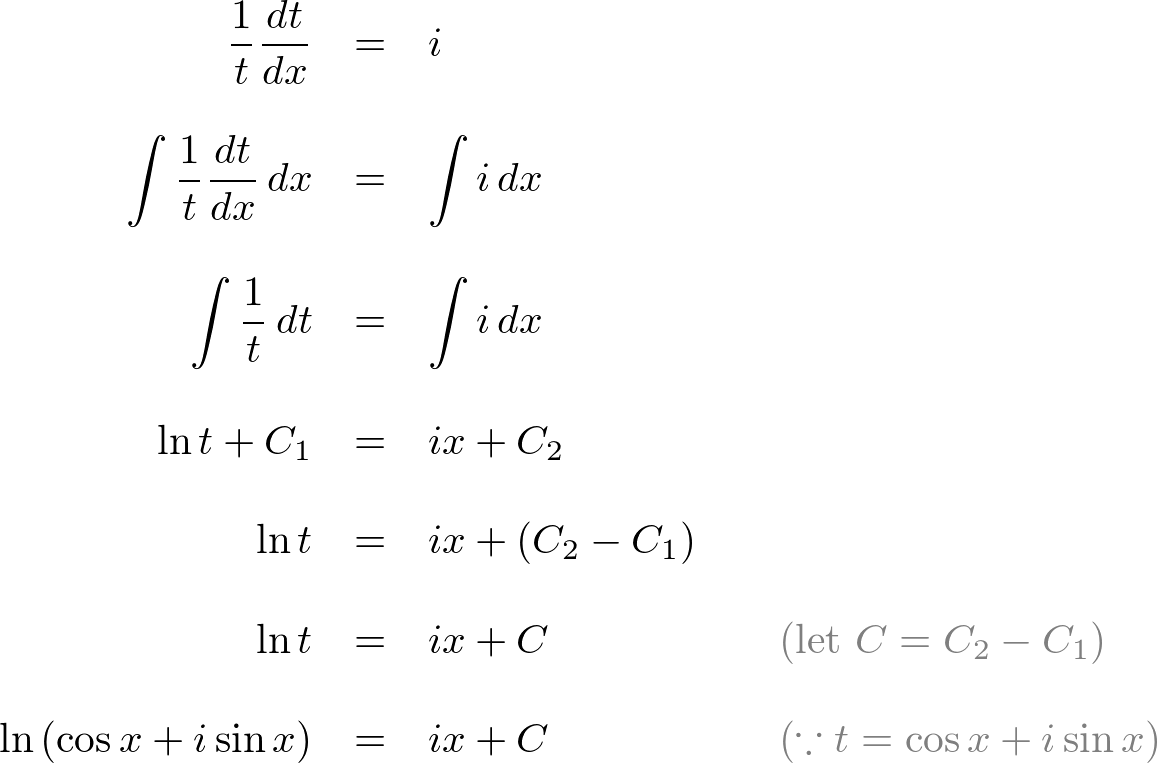
To find constant C, substitute x = 0:
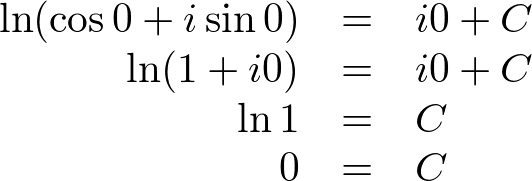
Now, we know C = 0, so the above equation is:
![]()
Finally, convert this logarithm form to the exponential form:
![]()