Quaternion to Rotation Matrix
Related Topics: Quaternion, OpenGL Rotation About Arbitrary Axis
Download: quaternion.zip
OpenGL API provides glRotatef() to rotate a 3D vector about an arbitrary axis using Rodrigues' rotation formula. Here explains how to convert Rodrigues' rotation formula to 4x4 matrix.
In addition, Quaternion can be also used for rotating a vector around an axis in 3D space. Multiplying Quaternions implies a rotation of a vector in 3D space and it is commonly used in 3D computer graphics algorithms because it is simpler and cheaper than the matrix multiplication. This page is focused on how to convert a Quaternion rotation to a 4x4 rotation matrix form using Quaternion algebra. Note that OpenGL accepts only 4x4 matrix to transform vertices.
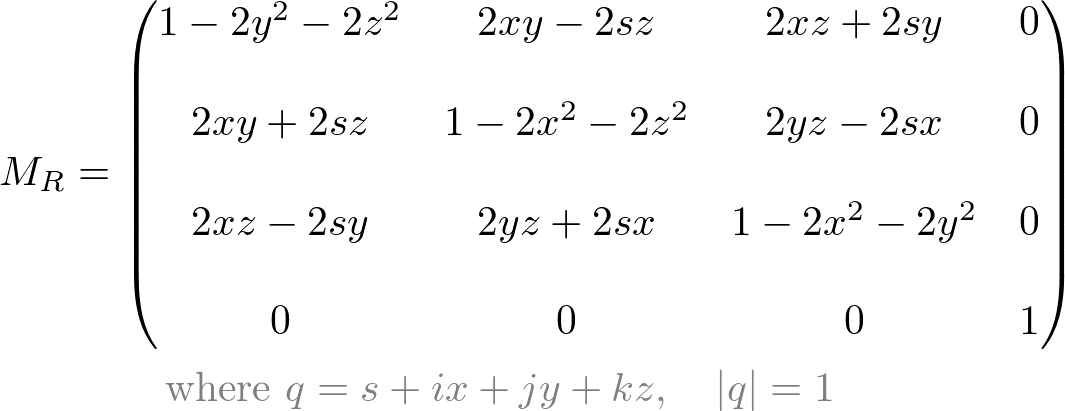
Overview
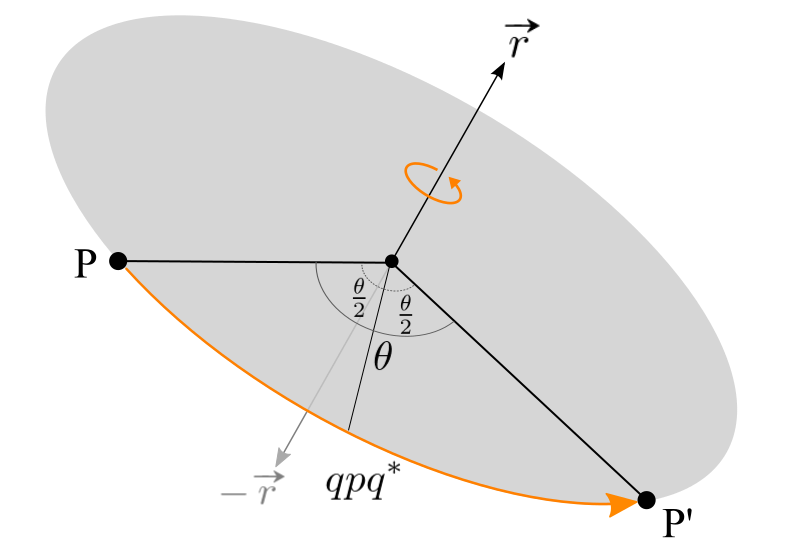
Suppose there is a 3D vector, 
and rotate it along an arbitrary axis (unit vector) 
by angle 
.
The vector 
can be converted as Quaternion form;
(We only use x, y and z components for .)
And, the Quaternion representation for the rotation axis vector 
and the half rotation angle 
can be written as;
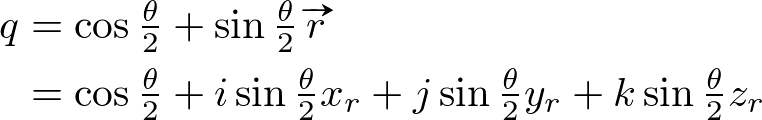
(Note that we only uses half angle to define the rotation quaternion q because we are going to multiply q twice.)
To rotate the quaternion p, we simply multiply the quaternion q. However, the length of p is changed during multiplication, so we multiply q* (conjugate of q) again at the back of p in order to cancel out the length changes. Since we multiply q twice, front and back, we only need a half rotation angle for q. Therefore, the final equation for the rotation in Quaternion becomes 
.
This special double multiplication is called "conjugation by q". Here explains why this double multiplication is required and the proof of the length conservation.
Quaternion to Matrix
In this section, we calculate using arbitrary Quaternions, p and q, then convert the result into a matrix form. Let's say p and q are defined as below, and q is normalized (
);
For a typical usage, rotating a 3D vector, we can set the scalar component to 0 for p. It makes the multiplication simpler, but here we use a generic 4-component quaternion for p.
First we multiply p by q (applying q on p);
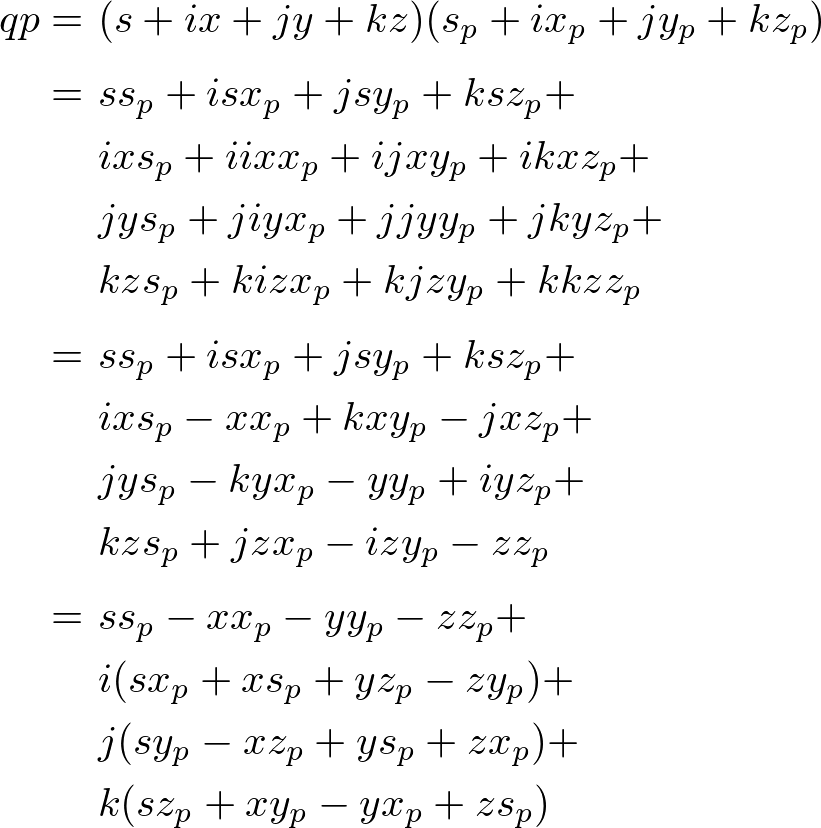
The above equation is simplified by Quaternion quadrantal (perpendicular) vectors property.
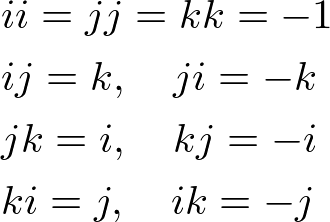
Let's set each component of 
to 
, 
, 
and 
respectively.
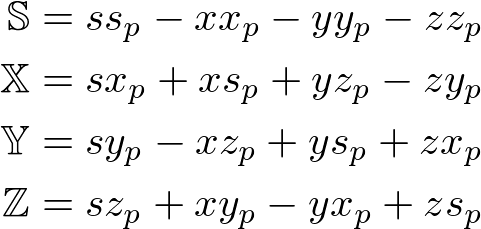
Then, multiply the conjugate of q at the back of the previous multiplication.
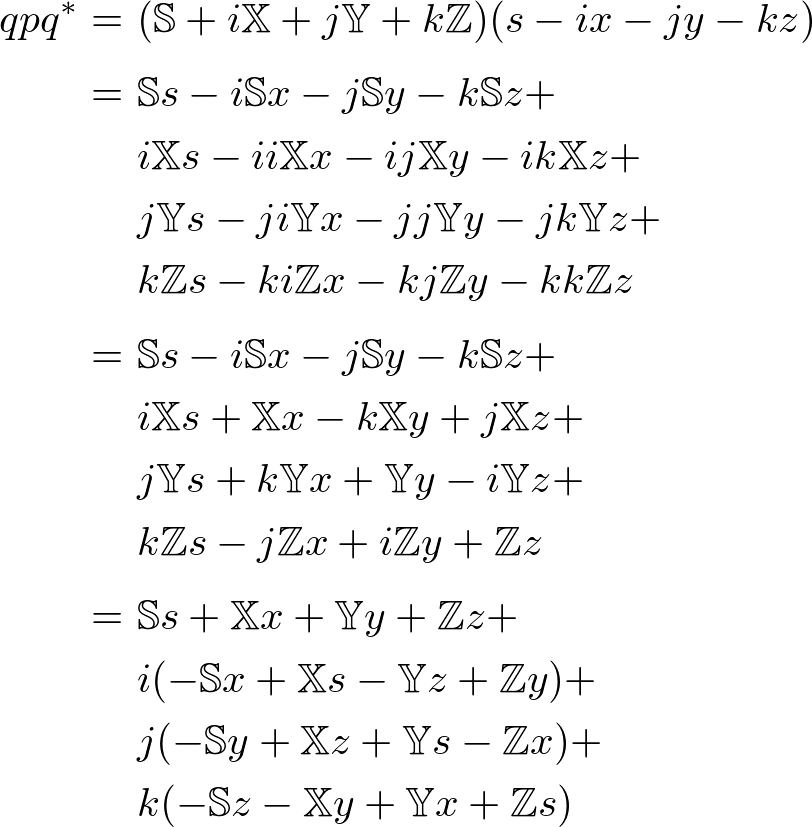
Since the equation becomes too long, we compute each term and component independently and combine them later. This page provides the complete computation of . You may skip to the final result of below.
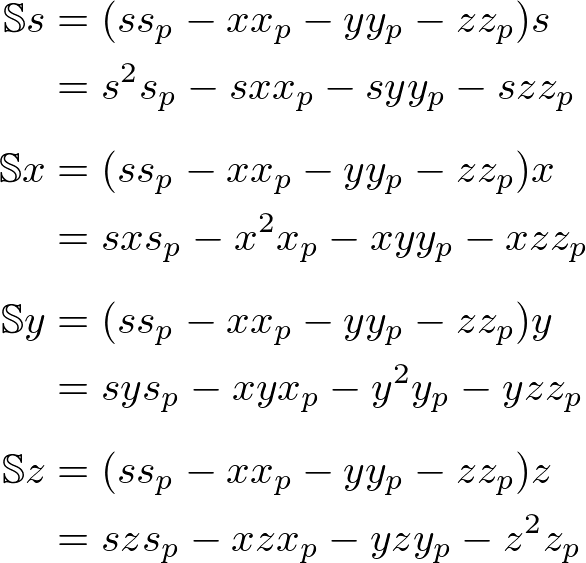
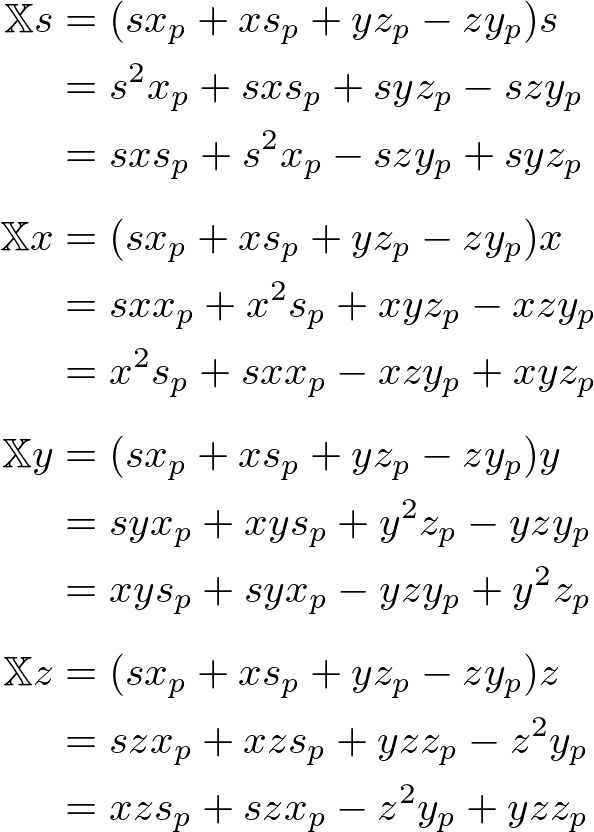
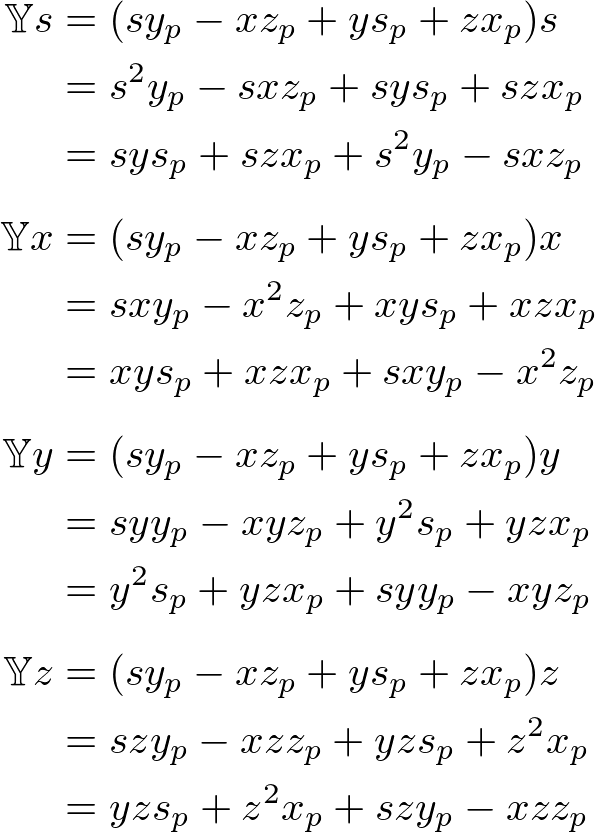
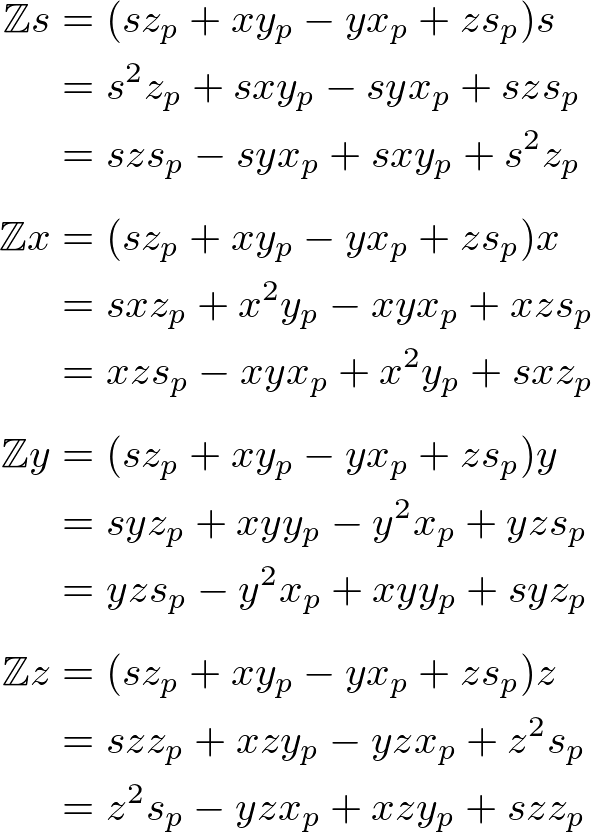
The scalar component of ;
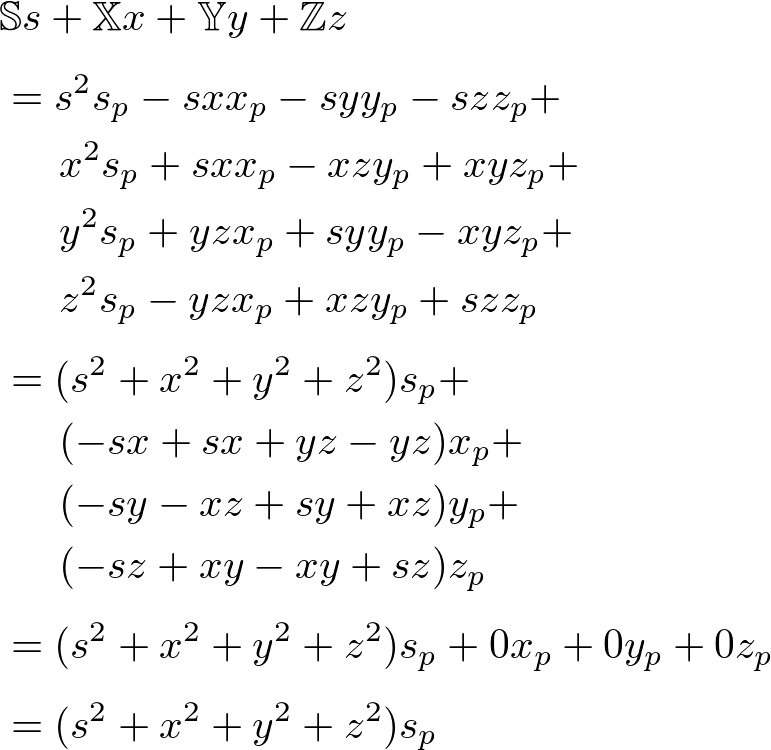
The x component of ;
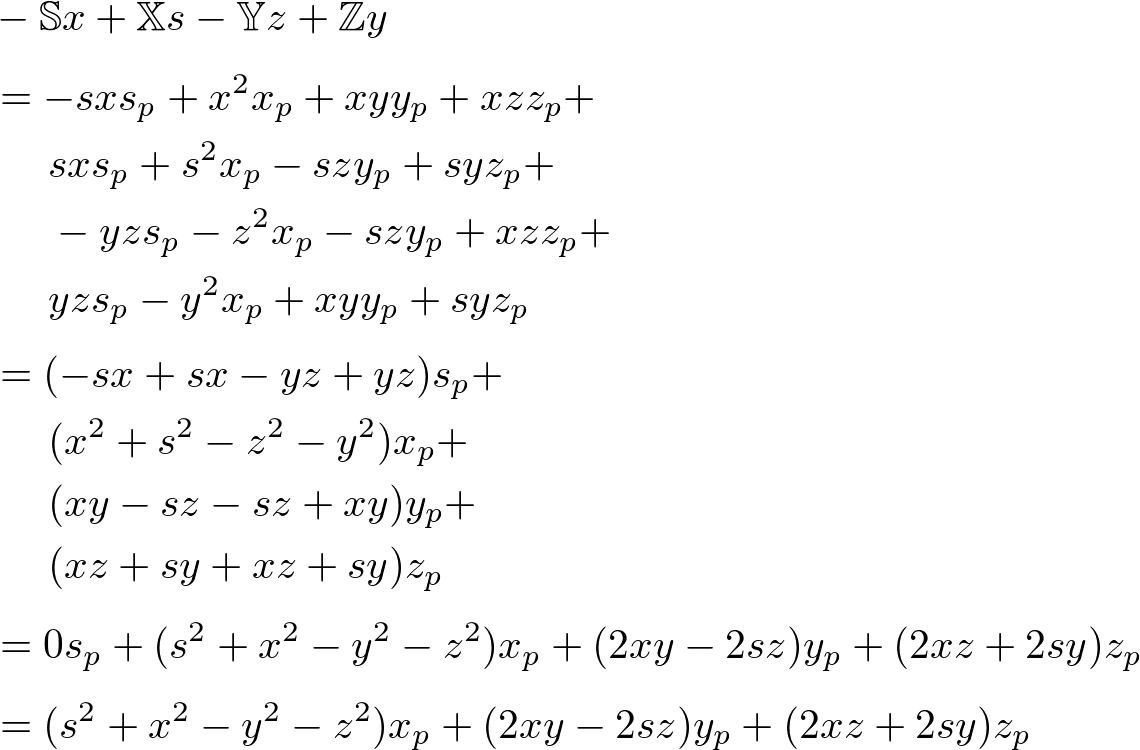
The y component of ;
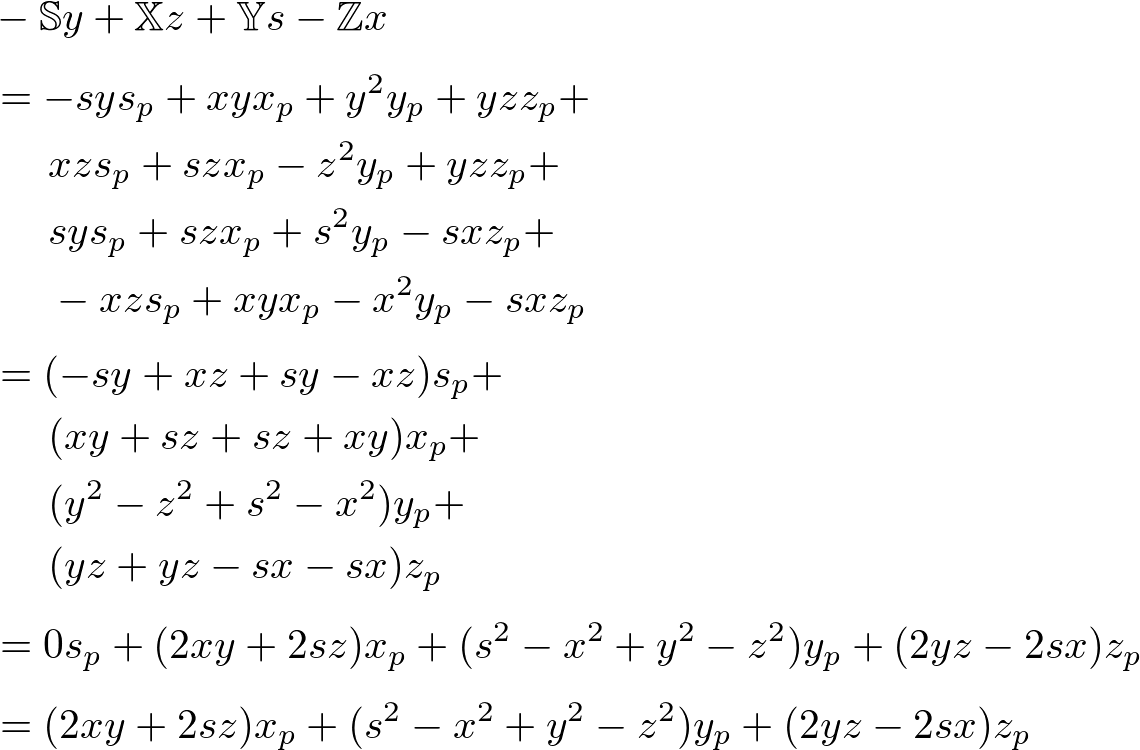
The z component of ;
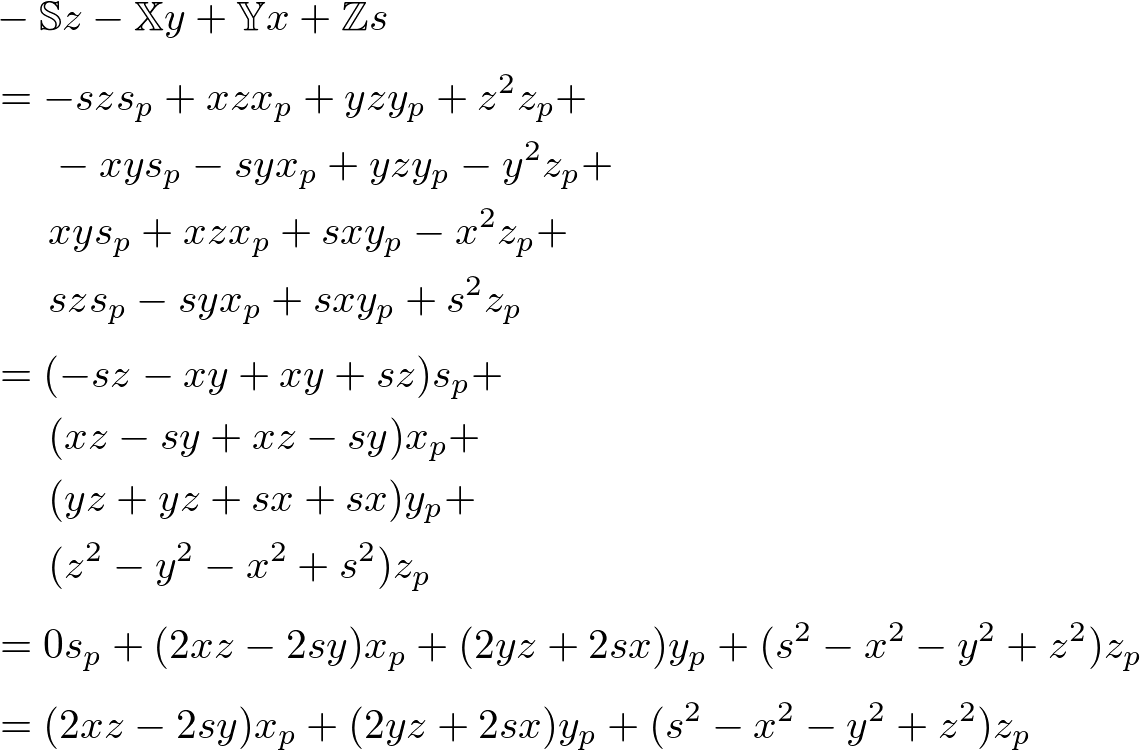
Finally, combine s, x, y and z components into the rotation quaternion, ;
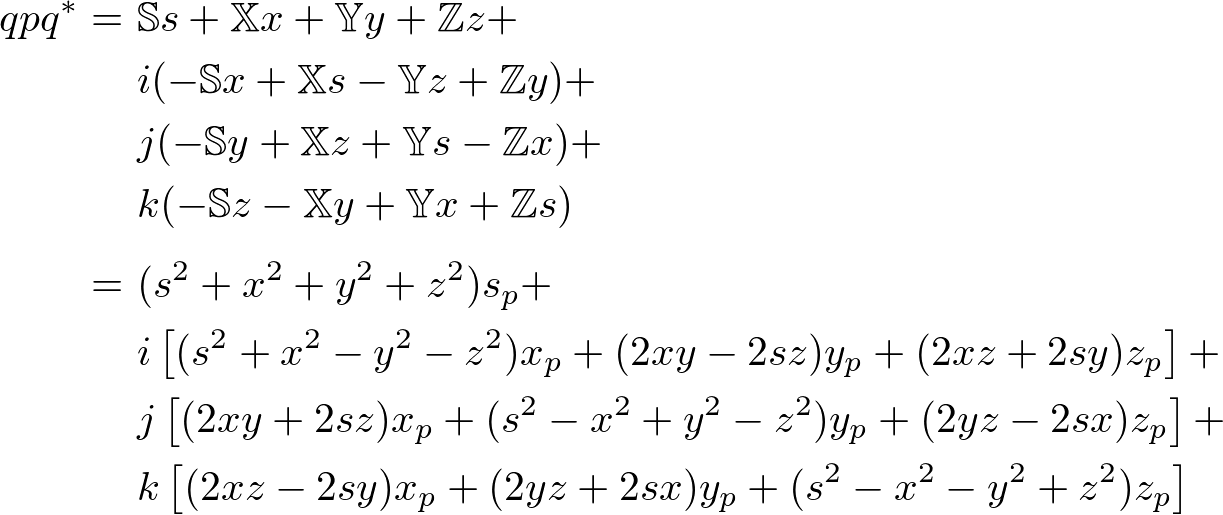
Since q is a unit quaternion, substitute the followings to the above equation to simplify it a little further.
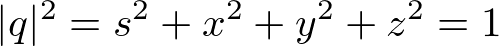
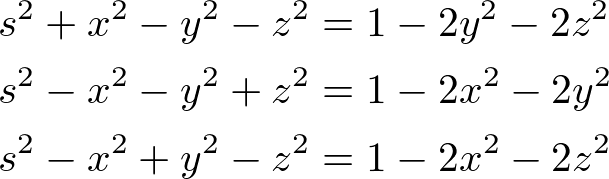
The final simplified rotation quaternion becomes;
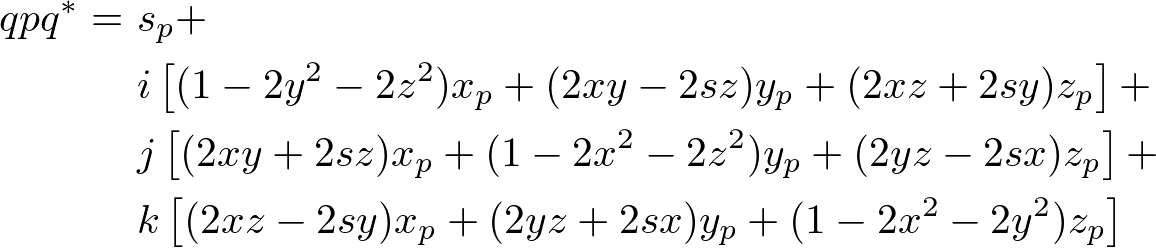
Now, we only take the x, y and z compoments (without i, j and k), and convert it to a matrix form. It becomes multiplying a 3x3 matrix to a 3D vector to transform.
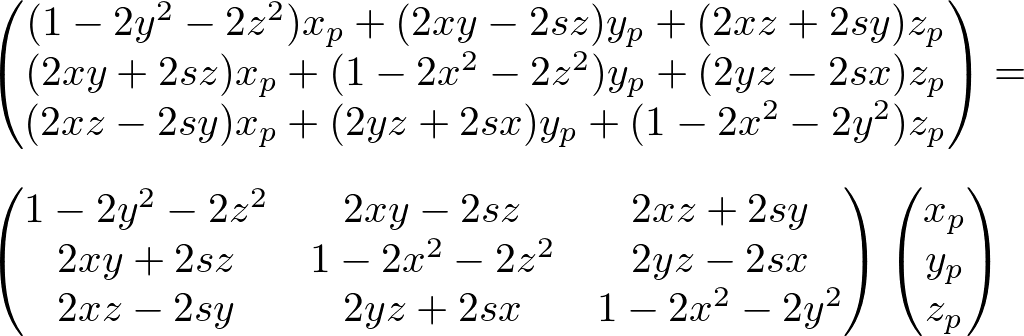
The 3x3 matrix itself is the rotation matrix equivalent to the quaternion rotation;
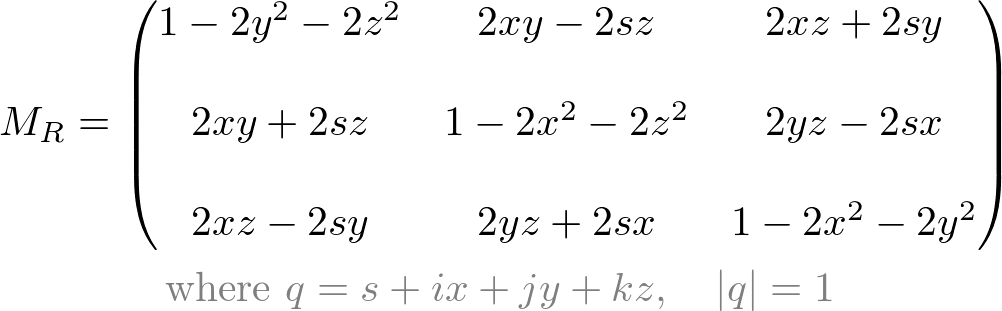
Or, as 4x4 matrix;
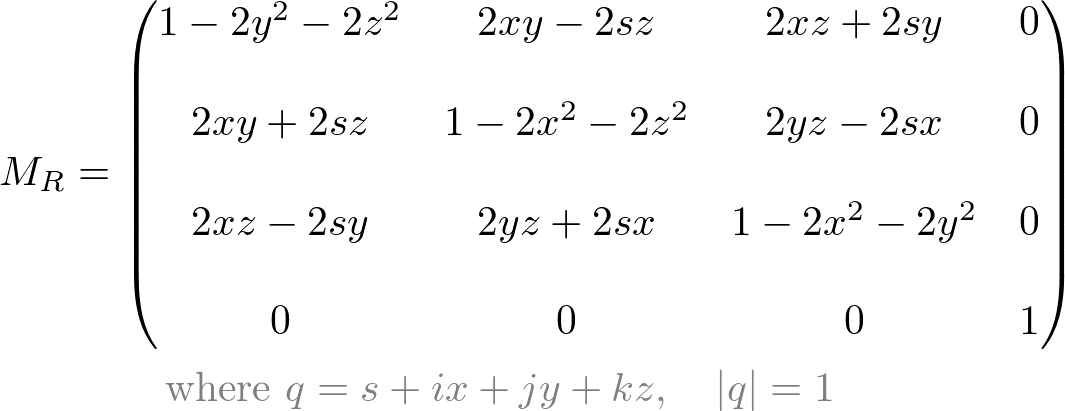
Example: Rotation with Quaternion
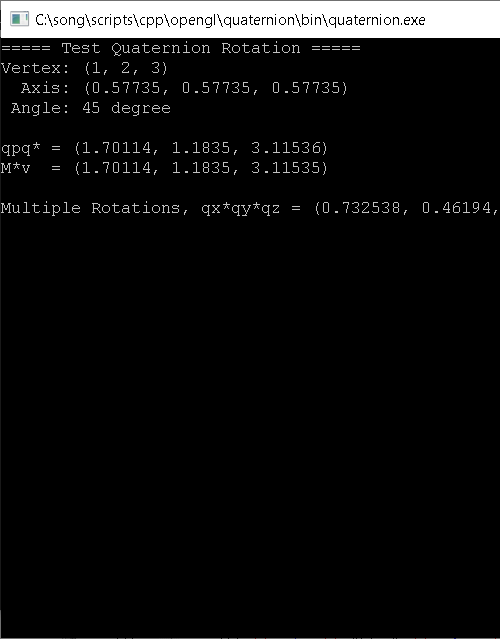
Download: quaternion.zip (Updated: 2023-03-05)
This example provides C++ Quaternion class and tests rotating a vertex, (1, 2, 3) along a rotation axis, (0.57735, 0.57735, 0.57735) by 45 degree. We need to convert the vertex and rotation axis to quaternion forms first, then rotate it with quaternion multiplication, . The Quaternion class provides getMatrix() to convert the rotation quaternion to 4x4 matrix form. It verifies the rotation result by comparing with rotation matrix.
Vector3 v(1, 2, 3); // 3D vertex to rotate
Vector3 r(0.57735f, 0.57735f, 0.57735f); // rotation axis (unit vector)
float a = 45.0f; // rotation angle in degree
// convert to quaternions
Quaternion p = Quaternion(0, v.x, v.y, v.z); // quaternion form of v
Quaternion q = Quaternion(r, a * 0.5f * D2R); // rotation quaternion with half-angle
Quaternion c = q; // copy of q
c.conjugate(); // q* (conjugate of q)
// rotate p by multiplying qpq*
Quaternion p2 = q * p * c;
// vector part of p2 contains the rotated 3D vertex
Vector3 v2(p2.x, p2.y, p2.z); // quaternion to vector
std::cout << "v2: " << v2 << std::endl; // print the result
// OR, convert quaternion to 4x4 roatation matrix
Matrix4 m = q.getMatrix();
v2 = m * v; // rotation using matrix instead
// OR, use matrix rotation directly
Matrix4 m
m.rotate(a, r); // rotate A degree along R axis
v2 = m * v; // rotation using matrix instead
If there is a sequence of multiple rotations, we can simply multiply the quaternions one after another, similar to matrix transformations. Multiplication of 2 quaternions requires 16 products and 12 additions. On the contrary, multiplying two 4x4 matrices needs 64 products and 48 additions.
// 3 rotations in quaternion form
Quaternion qx = Quaternion(Vector3(1, 0, 0), 22.5f * D2R); // 45 degree about x-axis
Quaternion qy = Quaternion(Vector3(0, 1, 0), 22.5f * D2R); // 45 degree about y-axis
Quaternion qz = Quaternion(Vector3(0, 0, 1), 22.5f * D2R); // 45 degree about z-axis
// compose multiple rotations, order is qz -> qy -> qx
Quaternion q = qx * qy * qz;
std::cout << "q: " << q << std::endl; // print the result
std::cout << q.getMatrix() << std::endl; // compare the result with matrixform below
// 3 rotations in matrix form
Matrix4 mx = Matrix4().rotateX(45.0f); // 45 degree about x-axis
Matrix4 my = Matrix4().rotateY(45.0f); // 45 degree about y-axis
Matrix4 mz = Matrix4().rotateZ(45.0f); // 45 degree about z-axis
// multiple matrix rotations, order is mz -> my -> mx
Matrix4 m = mx * my * mz;
std::cout << "m:\n" << m << std::endl; // compare the matrix result with the quaternion
