Quaternion

Related Topics: Euler's Equation, Quaternion to Rotation Matrix


quaternion

Quaternion is a geometrical operator to represent the relationship (relative length and relative orientation) between two vectors in 3D space. William Hamilton invented Quaternion and completed the calculus of Quaternions to generalize complex numbers in 4 dimension (one real part and 3 imaginary numbers). In this article, we focus on rotations of 3D vectors because Quaternion implementation for 3D rotation is usually simpler, cheaper and better behaved than other methods.

Background of Quaternion

Euler's equation (formula) can be used to represent a 2D point with a length and angle on a complex plane. Multiplication of 2 complex numbers implies a rotation in 2D. One may think instantly it can be extended to 3D rotation by adding additional dimension. William Hamilton initially studied it by adding an additional imaginary number, j to generalize complex numbers to 3D.

However, the set of 3 dimensional complex numbers is not closed under multiplication. For example, the multiplication of i and j cannot be represented as a form of a+ib+jc. If multiplication is closed, then there exist a, b, c ∈ R that satisfies ij=a+ib+jc.

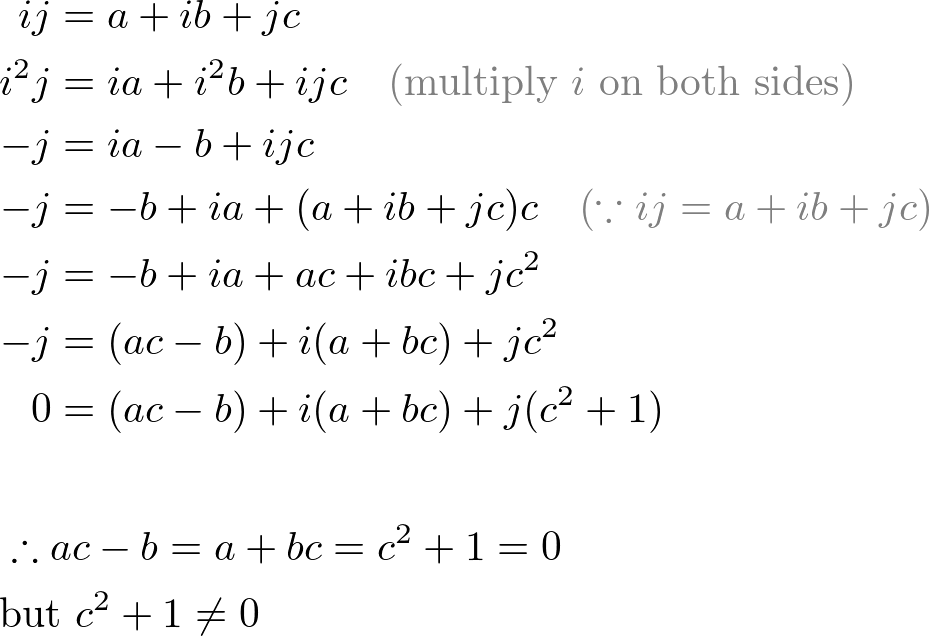
The equation c2+1=0 gives the contradiction. There is no real number c to satisfy c2+1=0 (It should be an imaginary number).

Later, Hamilton realized 4 dimensional complex numbers are required for multiplication to be closed by adding an additional imaginary part, k. And, he denoted this 4D complex number set as Quaternion. (In mathematics, each algebra has twice the dimension of the previous one. Therefore, the higher number set of complex number is quaternion, and the next number set is octonion.)

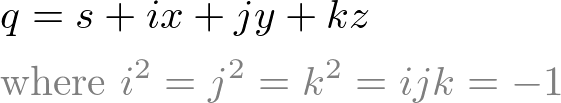
Now, the above example satisfies as ij = 0+i0+j0+k1, which ij is another imaginary number, ij = k. The condition of these 3 imaginary numbers is explained later, in Quadrantal vectors section.

Understanding of Quaternion

Definition

definition of quaternion
Definition of Quaternion operator

Hamilton's motivation was to create a geometrical operator to transform from a vector to the other in 3D space. This operator is the geometric quotient (ratio) between two vectors that changes the length and the orientation, and it is called a Quaternion because the operation is required 4 parameters.
quaternion definition, or,
(Note that this notation is not same as numerical division nor multiplication. Instead, it is translated as "the quaternion operator q on vector a to produce vector b, or the operator q to convert a into vector b".)

Tensor and Versor

When vector a is transformed to vector vector b, quaternion operator performs 2 distinct operations:

  1. Tensor: scaling the length of 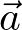vector a, so as to make it of the same length as b.
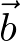  2. Versor: rotating vector a, so as to cause it to coincide with b in direction.

These 2 opearions can be symbolically represented Tensor(q) (tensor of q) and Versor(q) (versor of q) respectively.
q=Tensor(q)Versor(q)

The order of these two operations does not make any difference of the result. The combined tensor and versor operation requires 4 numbers; 1 for scaling, 1 for rotation angle, 2 additional angles to determine the orientation of the rotation plane. For example, a xy-plane is rotated about x and y axis. But, rotation along z axis does not change the orientation of the xy plane.

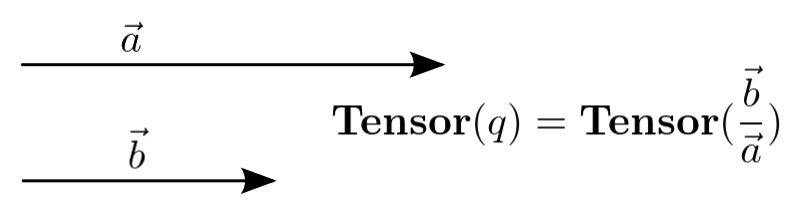
tensor of quaternion
Tensor operator

Tensor
Tensor of q is the geometric quotient (ratio) between the lengths of 2 parallel vectors. It changes the scale of the vector, but, keeps the orientation of the vector unchanged.

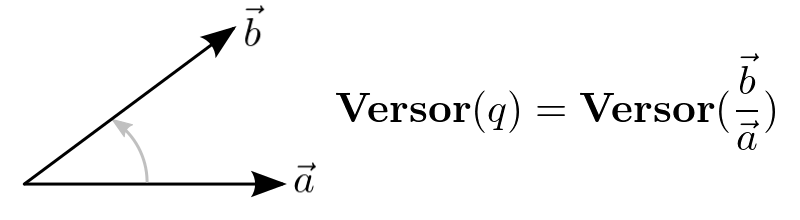
versor of quaternion
Versor operator

Versor
Versor of q is the geometric quotient of 2 non-parallel vectors of equal length. It represents the relative orientation of one vector with respect to the other vector, but, it does not change the length of the vector.

Expression with unit vectors

Quaternion with unit vectors

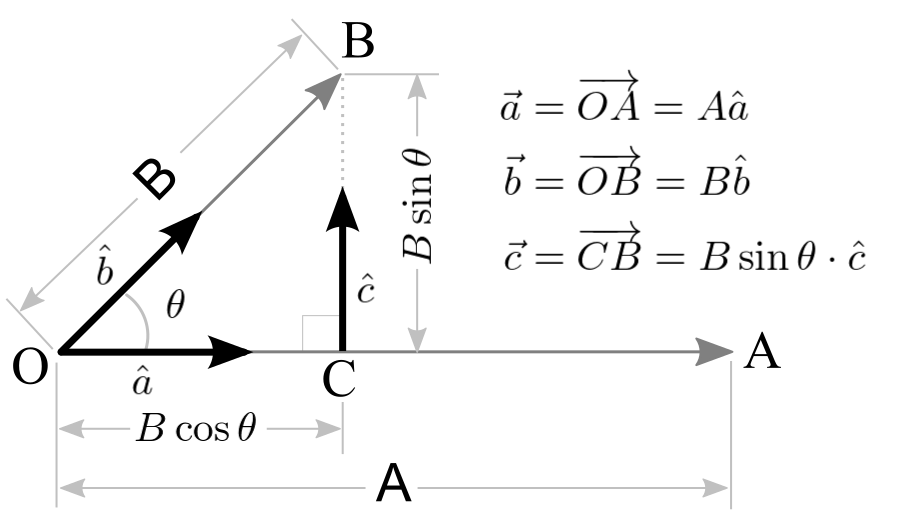
To investigate the quaternion operator deeper, let au and bu as unit vectors along a and b. so that

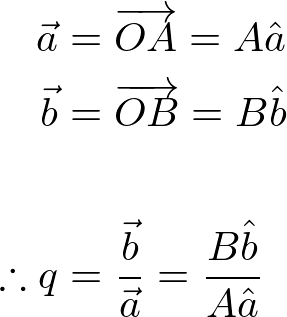
And, draw BC perpendicular to a, and let the unit vector along CB be cu. Therefore, OC becomes OC = B cos bu and CB = B sin cu . Since , we substitute OC and CB in the above equation, then we have a quaternion, q ;

Vector of Rotation axis

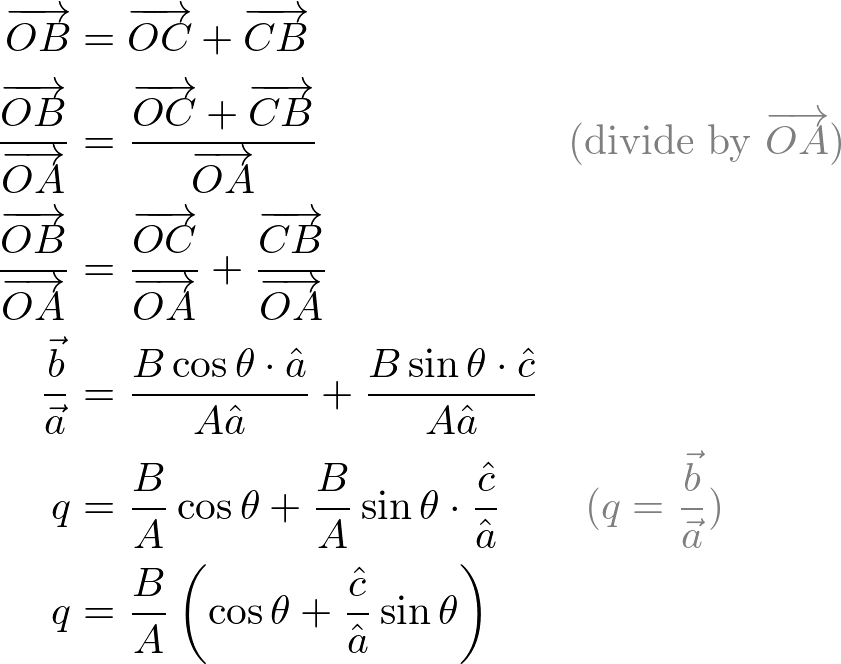
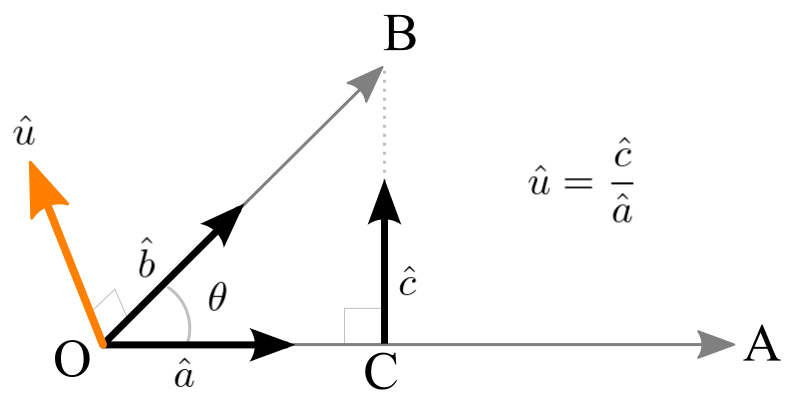
The last term contains the geometric quotient c/b of two unit vectors at right angles (90 degree) to each other. This quotient represents a unit vector perpendicular to the plane of au and cu. (Think of cross product of 2 vectors) This unit vector is indicating the rotation axis of the plane and the direction of rotation. If we define it u, the above equation becomes
A/B(cos + u sin)

From this equation, B/A is tensor (scaling) operation of a quaternion, and cos + u sin is versor (rotation) operator of a quaternion. Note that versor of q is very similar to Euler's equation. Euler's equation contains an imaginary number i, but a quaternion has a vector instead, which is the rotation axis perpendicular to its rotation plane.

Thus, a quaternion is also expressed as the sum of scalar S(q) and vector V(q) parts;
q=s+ix+jy+kz

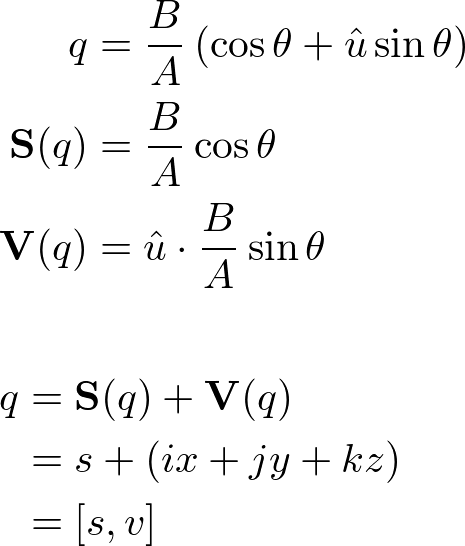
Quaternion can be also written as a 2-tuple form, [s, v]. A unit quaternion can be represented as [cos, usin], because the tensor of q is 1 (B/A = 1 or no scaling).

Quadrantal vectors: i, j, k

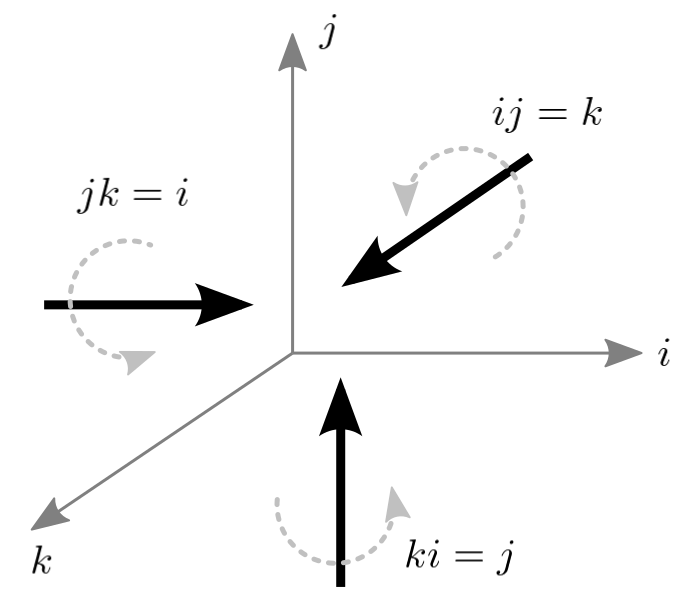
Quadrantal vectors
Quadrantal vectors

Let i, j and k represent unit vectors orthogonal (perpendicular) each other. We define multiplications and divisions as rotating a unit vector to another at right angle. Note that, this multiplication and division is not numeric algebra. This kind of multiplication and quotient is called geometric. Thus, production or quotient of two unit vectors at right angles to each other produces a unit vector, perpendicular to their plane. And, it reads as i operating on j (or, rotating from i to j) produces k.
ij=k

In same manner, we can write other multiplications and divisions;

The square of a unit vector can be defined from above equations;

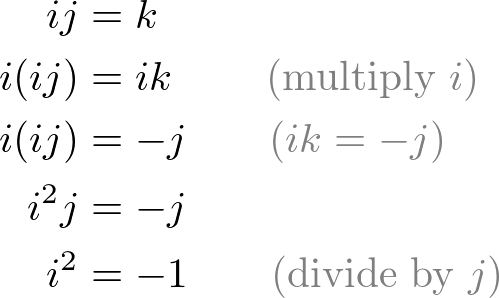
In same manner,
j^2=k^2=-1


Also, ijk can be defined as -1 using above multiplication table and square of unit vector.
ijk

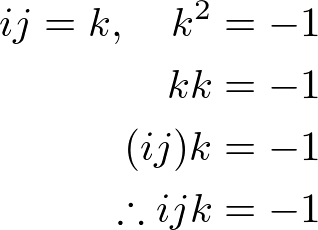
Quaternion Algebra

Here, the basic quaternion mathematics is described. These algebraic definitions and properties are specially required for rotation in 3D space, which describe in the next section. You may skip this section and move on the next section. And, come back later if you need to review a specific definition or property.

1. Addition

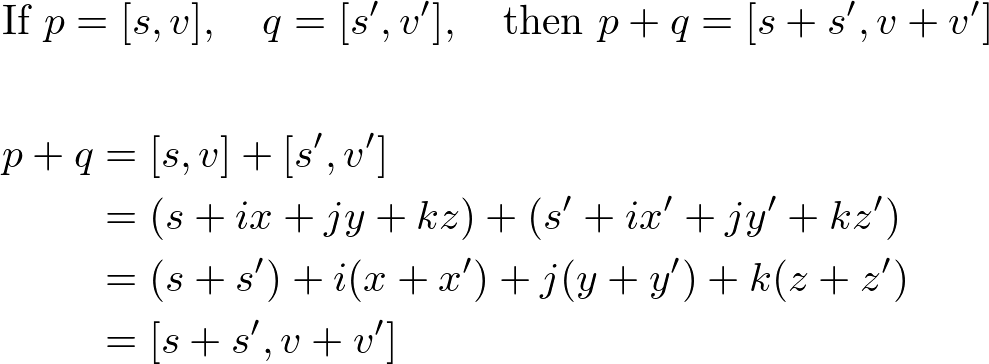
quaternion addition

2. Multiplication

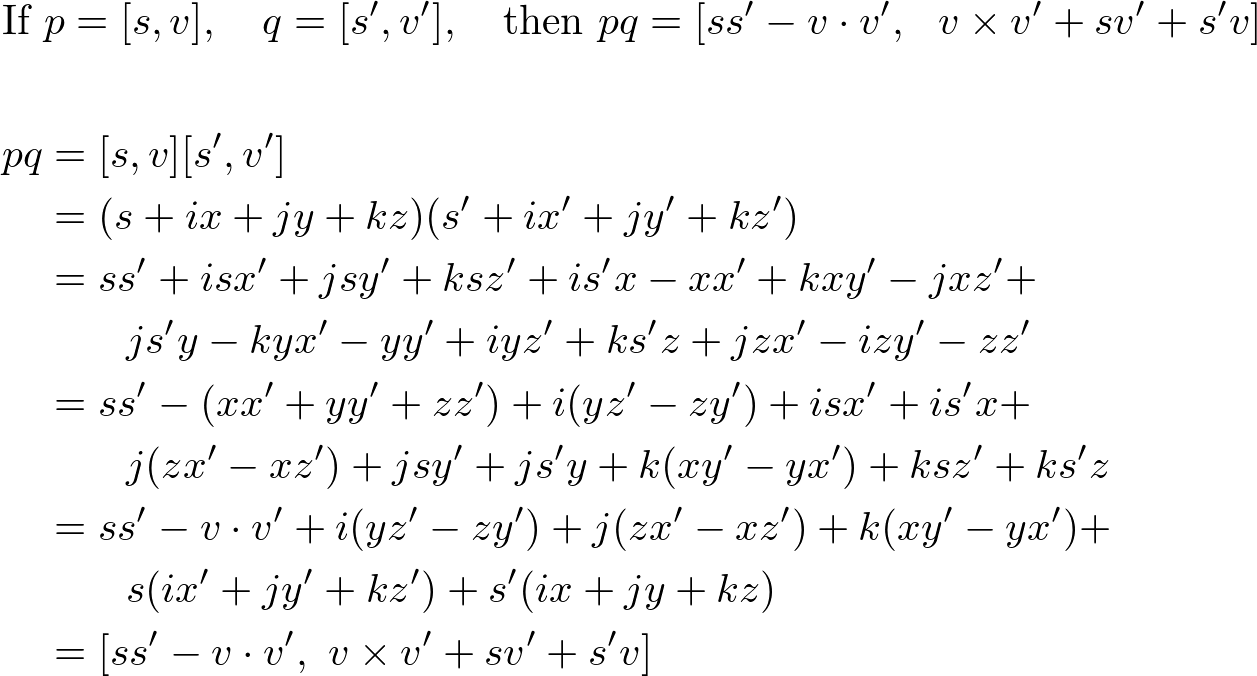
quaternion multiplication

Note that quaternion multiplication is not commutative, however, multiplication is associative and distributive across addition.

3. Scalar Multiplication

scalar multiplication

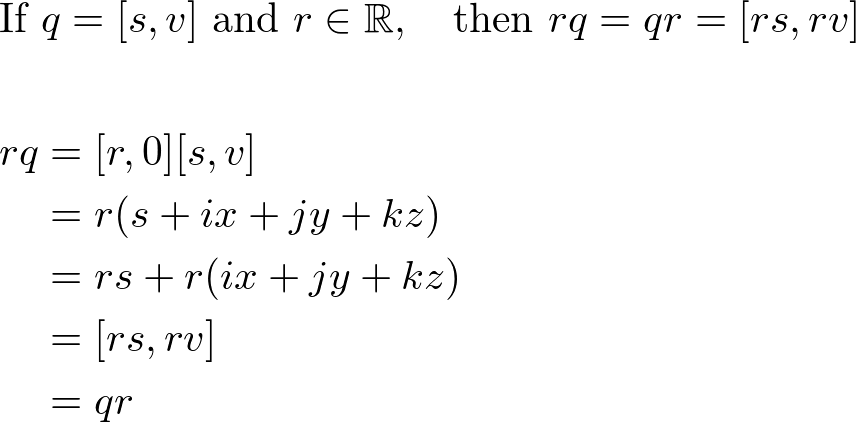
Unlike quaternion multiplication, scalar multiplication is commutative.

4. Subtraction

Quaternion subtraction can be derived from scalar multiplication and quaternion addition.
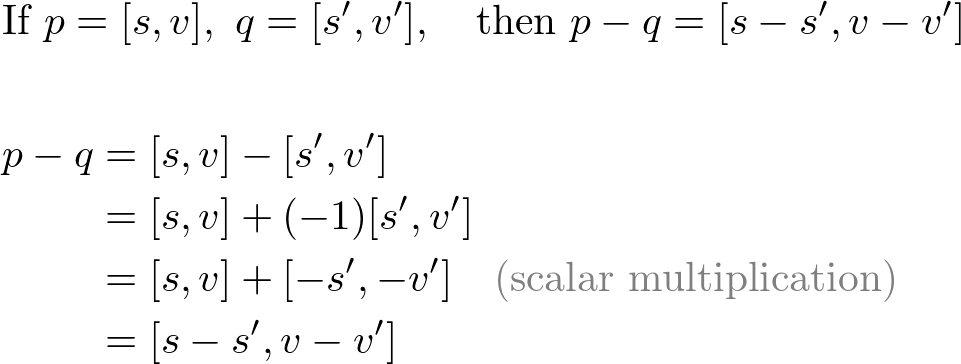
quaternion subtraction

5. Conjugate

Quaternion congugate is defined by negating the vector part of the quaternion.
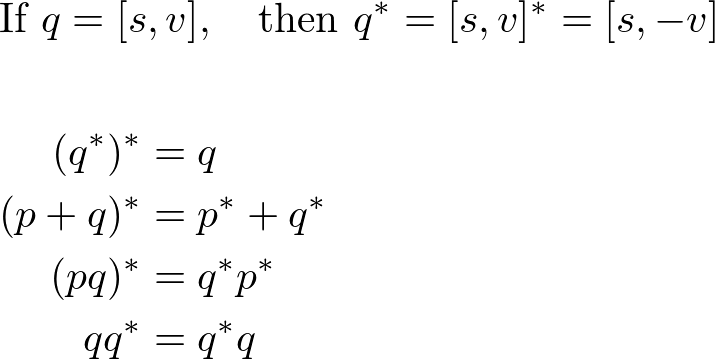
quaternion conjugate
Note that the multiplication of a quaternion and its conjugate is commutative.

6. Norm (Length)

The norm of a quaternion is defined by;
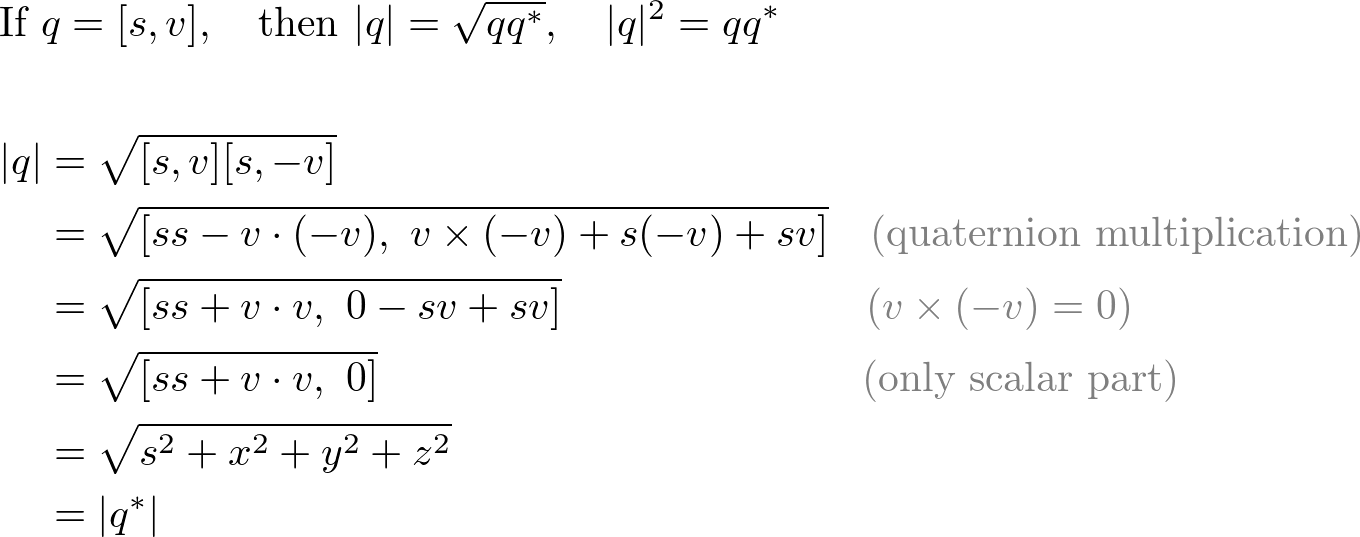
quaternion norm

The norm of quaternion is multiplicative meaning that the norm of the multiplication of multiple quaternions equals to the multiplication of the norms of quaternions.
quaternion norm multiplicative

7. Inverse

The inverse of a quaternion is defined to be;
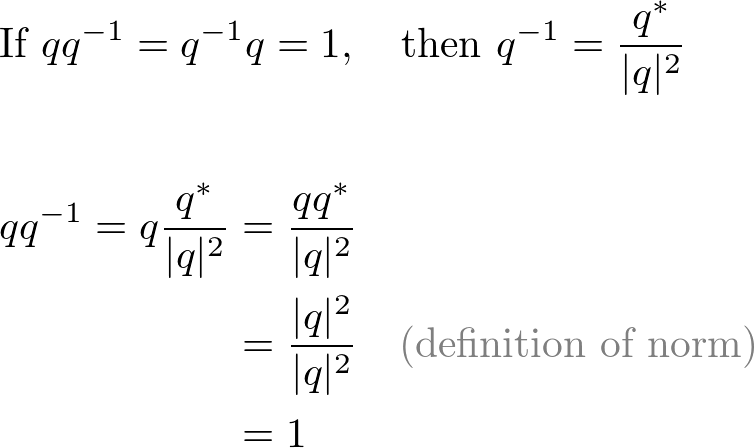
quaternion inverse
The quaternion inverse makes it possible to divide two quaternions.

8. Unit Quaternion

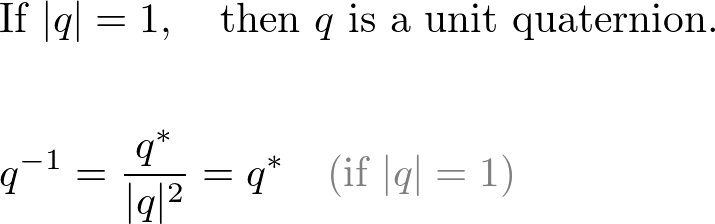
unit quaternion
Note that the inverse of a unit quaternion equals to the conjugate of the unit quaternion.

3D Rotation with Quaternion

In 2D, the multiplication of two complex numbers implies 2D rotation. When z=x+iy is multiplied by , the length of z' remains same (|z|=|z'|), and the angle of z' is simply added by θ. (See details in Euler's equation.)

However, multiplying a quaternion p by another quaternion q does not conserve the length (norm) of the vector part of the quaternion p even if q is a unit quaternion. For example;

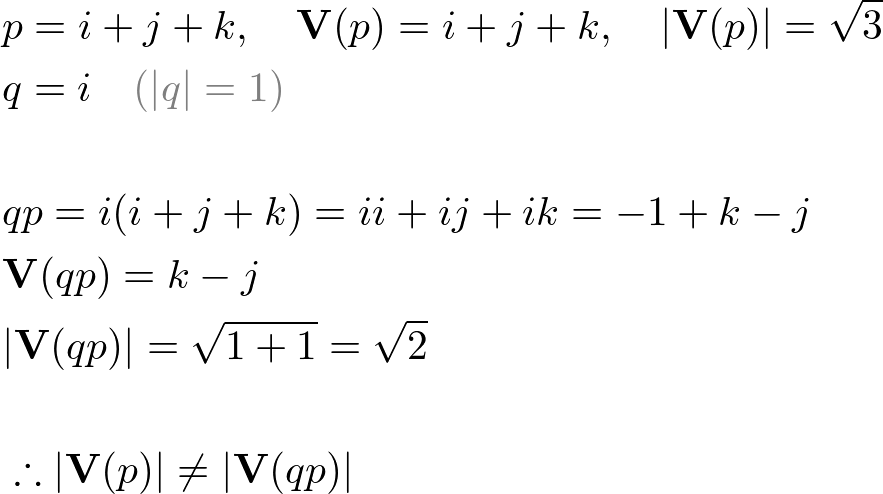
Thus, we need a special multiplication for 3D rotations that is length-conserving transformation. For this reason, we multiply the quaternion q at the front of p and multiplying its inverse q-1 at the back of p, in order to cancel out the length changes. This special double multiplication is called "conjugation by q".

If a quaternion is p = [s, v], then the scalar (s) and the length of v, |v| are unchanged after conjugation by q. For the above example;

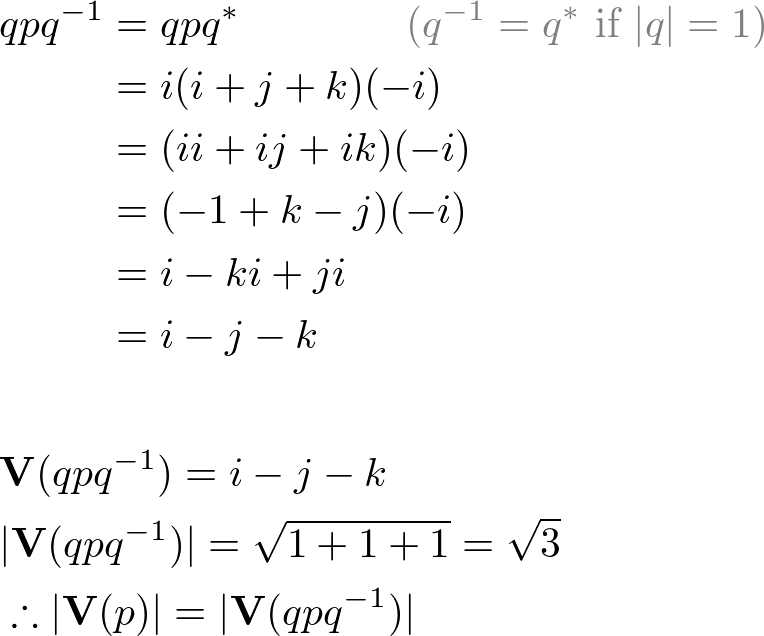
Proof

If p = [s, v] and p' = qpq-1, then p' = [s, v'] where |v| = |v'|.
(The scalar part of p' is same as p and the length of the vector part is also unchanged.)

The proof takes 4 steps. First, we show the scalar parts of quaternions, S(p)=S(p') for p=[s, 0], and for p=[0, v]. Then, both results are used to show S(p)=S(p') for p=[s, v]=[s, 0]+[0, v]. Finally, we show the length of p' is unchanged (conserved), therefore, the length of the vector part is same, |V(p)| = |V(p')|.

Step 1. If p has a scalar part only p = [s, 0], then

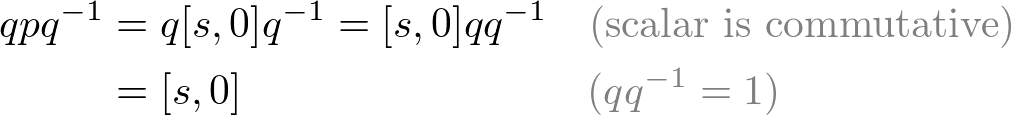
Step 2. If p has a vector part only p = [0, v], then the scalar part of qpq-1 can be computed by 2S(p)=p+p*.

Step 3. If p = [s, v] = [s, 0] + [0, v], then S(p) = S(p').

Step 4. The norm of p' is same as the norm of p;

 

Since the lengths and the scalar parts of p and p' are same, the lengths of the vector parts are also same;

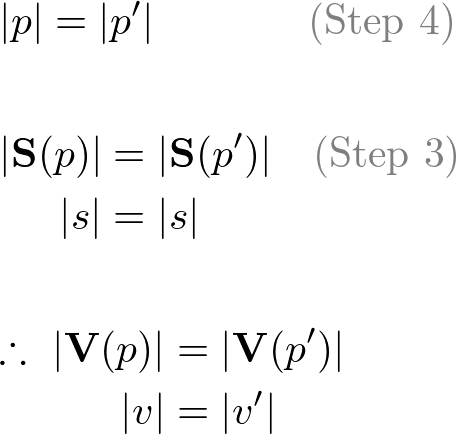
Quaternion to Matrix

The rotation with quaternion by can be expressed with matrix from;
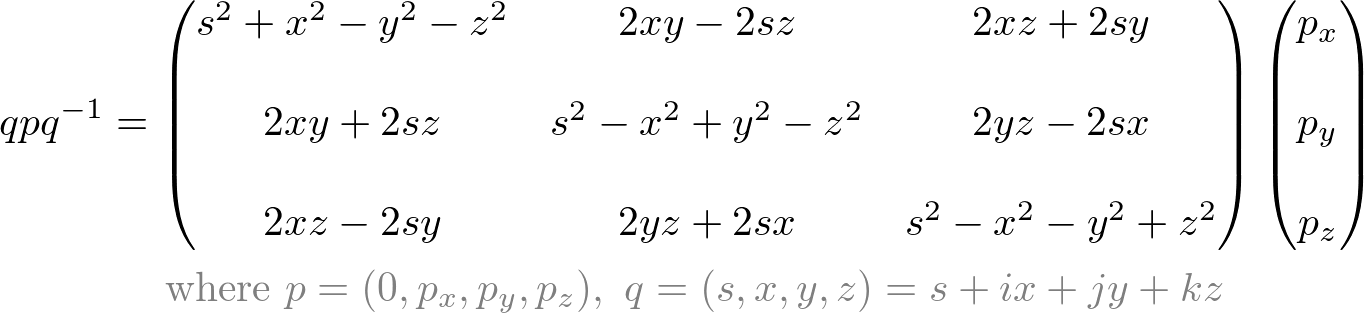
quaternion to matrix

If q is a unit quaternion, it can be simplified by;
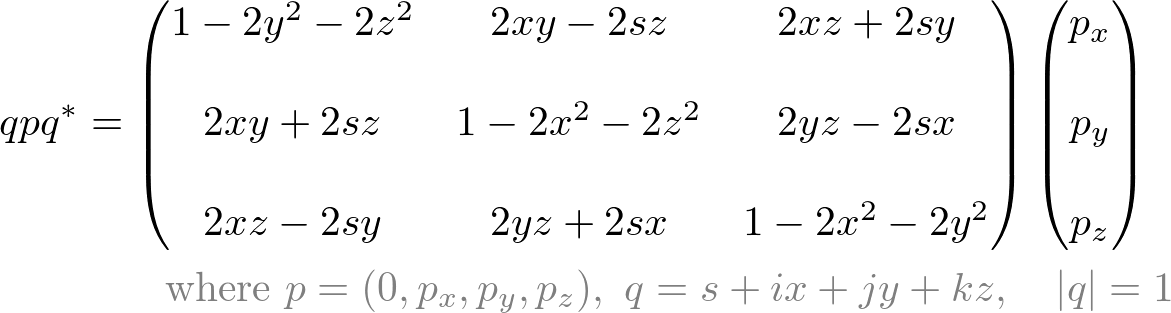
quaternion to matrix

The derivation of matrix conversion is explained at Quaternion to OpenGL Matrix.

References

  • A. S. Hardy (1881). Elements of Quaternions
  • E. B. Dam, M. Koch, M. Lillholm (1998). Quaternions, Interpolation and Animation
←Back
 
Hide Comments
comments powered by Disqus