Torus, Torus Knot & Trefoil Knot
Related Topics: OpenGL Sphere, OpenGL Cylinder, Prism & Pipe
Download: torus.zip, torusShader.zip, torusKnot.zip, torusKnotShader.zip
- Torus
- Example: Drawing Torus
- Example: WebGL Torus (Interactive Demo)
- Torus Knot
- Example: Drawing Torus Knot
- Example: WebGL Torus Knot (Interactive Demo)
- Trefoil Knot
- Example: Drawing Trefoil Knot
- Example: WebGL Trefoil Knot (Interactive Demo)
This page describes how to generate a torus and torus knot geometries using C++ and how to draw it with OpenGL.
Torus
A torus is a ring-like 3D geometry by revolving a circle around a circular path. The radius of the circle is called the minor radius, r. And, the radius of the circular path is called the major radius, R which is the distance from the origin to the center of the circle.

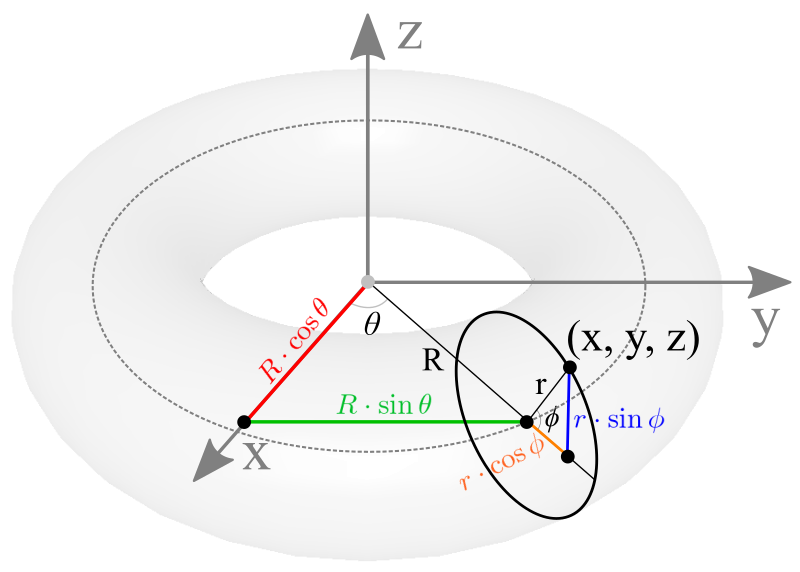
An arbitrary point (x, y, z) on a torus can be computed by the parametric equations with the major radius R, minor radius r, and the corresponding sector and side angles θ and ϕ.
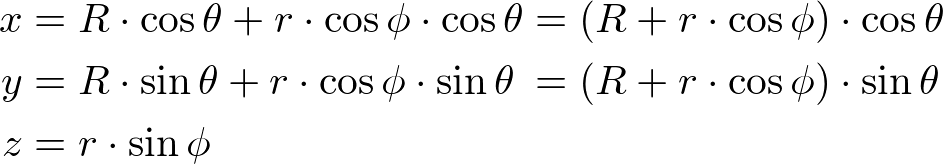
Due to limited resources, we only use a limited number of sectors for the circular path and the sides for the circle itself to approximate the 3D geometry. The range of sector angles is from 0 to 360 degrees, and the side angle of the circle is from 180 to -180 degrees. The sector and side angle for each step can be calculated by the following;
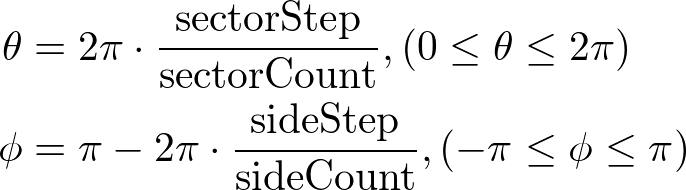
The following C++ code generates all vertices of the torus for the given radii, sectors and sides. It also creates other vertex attributes; surface normals, texture coordinates and indices. For more details, please refer to buildVerticesSmooth() or buildVerticesFlat() functions in Torus.cpp class.
// x = (R + r * cos(u)) * cos(v) = R * cos(v) + r * cos(u) * cos(v)
// y = (R + r * cos(u)) * sin(v) = R * sin(v) + r * cos(u) * sin(v)
// z = r * sin(u)
// where u: side angle (-180 ~ 180)
// v: sector angle (0 ~ 360)
// clear memory of prev arrays
std::vector<float>().swap(vertices);
std::vector<float>().swap(normals);
std::vector<float>().swap(texCoords);
std::vector<unsigned int>().swap(indices);
float x, y, z, xy; // vertex position
float nx, ny, nz; // normal
float lengthInv = 1.0f / minorRadius; // to normalize normals
float s, t; // texCoord
float sectorStep = 2 * PI / sectorCount;
float sideStep = 2 * PI / sideCount;
float sectorAngle, sideAngle;
for(int i = 0; i <= sideCount; ++i)
{
// start the tube side from the inside where sideAngle = pi
sideAngle = PI - i * sideStep; // starting from pi to -pi
xy = minorRadius * cosf(sideAngle); // r * cos(u)
z = minorRadius * sinf(sideAngle); // r * sin(u)
// add (sectorCount+1) vertices per side
// the first and last vertices have same position and normal,
// but different tex coords
for(int j = 0; j <= sectorCount; ++j)
{
sectorAngle = j * sectorStep; // starting from 0 to 2pi
// tmp x and y to compute normal vector
x = xy * cosf(sectorAngle);
y = xy * sinf(sectorAngle);
// add normalized vertex normal first
nx = x * lengthInv;
ny = y * lengthInv;
nz = z * lengthInv;
addNormal(nx, ny, nz);
// shift x & y, and vertex position
x += majorRadius * cosf(sectorAngle); // (R + r * cos(u)) * cos(v)
y += majorRadius * sinf(sectorAngle); // (R + r * cos(u)) * sin(v)
addVertex(x, y, z);
// vertex tex coord between [0, 1]
s = (float)j / sectorCount;
t = (float)i / sideCount;
addTexCoord(s, t);
}
}
// indices
// k1--k1+1
// | / |
// | / |
// k2--k2+1
unsigned int k1, k2;
for(int i = 0; i < sideCount; ++i)
{
k1 = i * (sectorCount + 1); // beginning of current side
k2 = k1 + sectorCount + 1; // beginning of next side
for(int j = 0; j < sectorCount; ++j, ++k1, ++k2)
{
// 2 triangles per sector
addIndices(k1, k2, k1+1); // k1---k2---k1+1
addIndices(k1+1, k2, k2+1); // k1+1---k2---k2+1
}
}
// add vertex attributes to arrays
void Torus::addVertex(float x, float y, float z)
{
vertices.push_back(x);
vertices.push_back(y);
vertices.push_back(z);
}
void Torus::addNormal(float nx, float ny, float nz)
{
normals.push_back(nx);
normals.push_back(ny);
normals.push_back(nz);
}
void Torus::addTexCoord(float s, float t)
{
texCoords.push_back(s);
texCoords.push_back(t);
}
void Torus::addIndices(unsigned int i1, unsigned int i2, unsigned int i3)
{
indices.push_back(i1);
indices.push_back(i2);
indices.push_back(i3);
}
Example: Torus
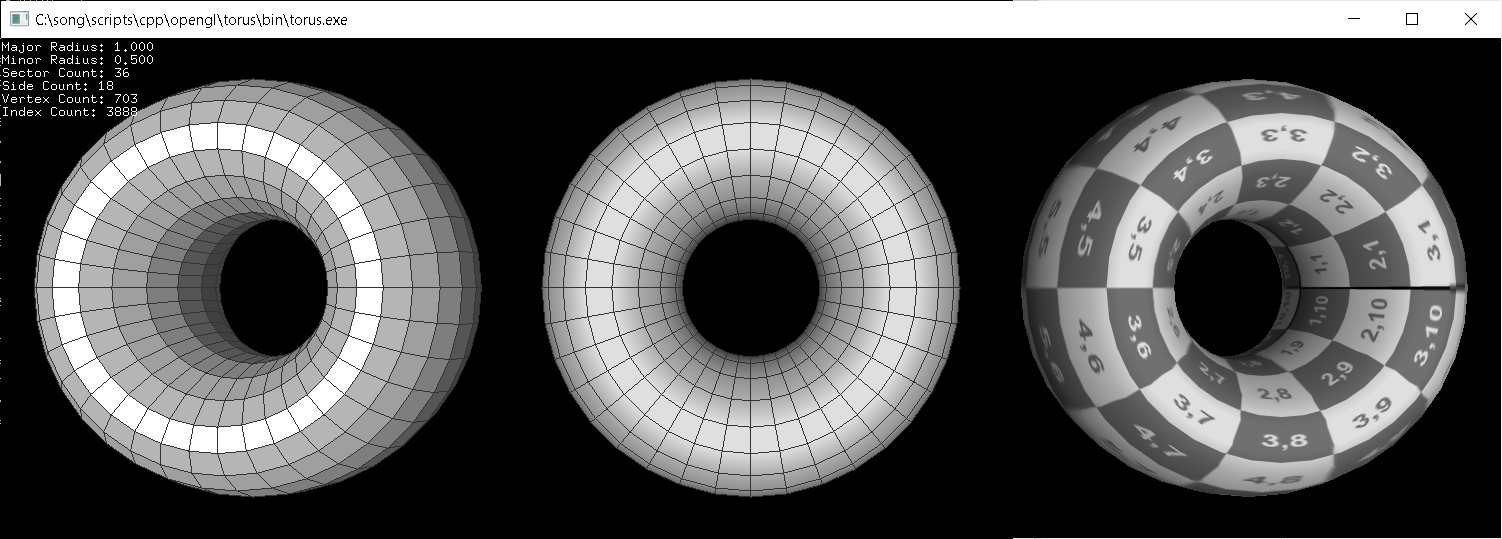
Download: torus.zip, torusShader.zip (with GLFW) (Updated: 2025-10-23)
This example constructs tori with major radius 1, minor radius 0.5, 36 sectors and 18 sides, but with different shadings; flat, smooth or textured. Torus.cpp class provides pre-defined functions; draw(), drawWithLines() and drawLines(), to draw a torus using OpenGL VertexArray.
By default, the revolving axis of the torus is +Z axis. But, it can be changed by the last parameter of Torus class contructor (X=1, Y=2, or Z=3), or by calling setUpAxis() function after it is constructed.
// create a torus with R=1, r=0.5, sectors=36, stacks=18, smooth=true, up=Z
Torus torus(1.0f, 0.5f, 36, 18);
Torus torus(1.0f, 0.5f, 36, 18, true, 3); // same as above
// can change parameters later
torus.setMajorRadius(2.0f);
torus.setMinorRadius(1.0f);
torus.setSectorCount(72);
torus.setSideCount(24);
torus.setSmooth(false);
torus.setUpAxis(2); // X=1, Y=2, Z=3
...
// draw torus using vertexarray
torus.draw();
This C++ class also provides getVertices(), getIndices(), getInterleavedVertices(), etc. in order to access the vertex data in GLSL. The following code draws a torus with interleaved vertex data using VBO, VAO and GLSL. Or, download torusShader.zip for more details.
// create a torus with default params; R=1, r=0.5, sectors=36, sides=18, smooth=true
Torus torus;
// creat VAO to store VBO states
GLuint vaoId;
glGenVertexArrays(1, &vaoId1);
glBindVertexArray(vaoId1);
// copy interleaved vertex data (V/N/T) to VBO
GLuint vboId;
glGenBuffers(1, &vboId);
glBindBuffer(GL_ARRAY_BUFFER, vboId); // for vertex data
glBufferData(GL_ARRAY_BUFFER, // target
torus.getInterleavedVertexSize(), // data size, # of bytes
torus.getInterleavedVertices(), // ptr to vertex data
GL_STATIC_DRAW); // usage
// copy index data to VBO
GLuint iboId;
glGenBuffers(1, &iboId);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, iboId); // for index data
glBufferData(GL_ELEMENT_ARRAY_BUFFER, // target
torus.getIndexSize(), // data size, # of bytes
torus.getIndices(), // ptr to index data
GL_STATIC_DRAW); // usage
// enable vertex array attributes for bound VAO
glEnableVertexAttribArray(attribPos);
glEnableVertexAttribArray(attribNorm);
glEnableVertexAttribArray(attribTex);
// store vertex array pointers to bound VAO
int stride = torus.getInterleavedStride();
glVertexAttribPointer(attribPos, 3, GL_FLOAT, false, stride, 0);
glVertexAttribPointer(attribNorm, 3, GL_FLOAT, false, stride, (void*)(3*sizeof(float)));
glVertexAttribPointer(attribTex, 2, GL_FLOAT, false, stride, (void*)(6*sizeof(float)));
...
// bind VAO before drawing
glBindVertexArray(vaoId);
// draw a torus with VBO
glDrawElements(GL_TRIANGLES, // primitive type
torus.getIndexCount(), // # of indices
GL_UNSIGNED_INT, // data type
(void*)0); // offset to indices
// unbind VAO
glBindVertexArray(0);
Example: WebGL Torus (Interactive Demo)
It is a JavaScript version of Torus class, Torus.js, and rendering it with WebGL. Drag the sliders to change the parameters of the totus. The fullscreen version is available at WebGL Torus.
The following JavaScript code is to create and to render a torus object.
// create a torus with 5 params: R, r, sectors, sides, smooth
let torus = new Torus(gl, 1, 0.5, 36, 18, false);
...
// change params of torus later
torus.setMajorRadius(2);
torus.setMinorRadius(3);
torus.setSectorCount(8);
torus.setSideCount(4);
torus.setSmooth(true);
torus.setUpAxis(2);
...
// draw a torus with interleaved mode
gl.bindBuffer(gl.ARRAY_BUFFER, torus.vboVertex);
gl.vertexAttribPointer(gl.program.attribPosition, 3, gl.FLOAT, false, torus.stride, 0);
gl.vertexAttribPointer(gl.program.attribNormal, 3, gl.FLOAT, false, torus.stride, 12);
gl.vertexAttribPointer(gl.program.attribTexCoord0, 2, gl.FLOAT, false, torus.stride, 24);
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, torus.vboIndex);
gl.drawElements(gl.TRIANGLES, torus.getIndexCount(), gl.UNSIGNED_SHORT, 0);
...
Torus Knot

A torus knot is a knot/path on the surface of a torus geometry by revolving around the major axis and hole of the torus. The number windings along the major axis is defined by p and the number of windings through the torus hole is q. For example, the image on the side shows (1,3)-torus knot with p=1 and q=3.
The parametric equation of the path of a torus knot is:

where R is the major radius, r is the minor radius of the torus.
Once you find the path on the torus with a (p,q) pair, you can draw a tube or contour following the path to construct 3D torus knot geometry.
One way to construct the 3D torus knot geometry is projecting the contour (circle) at the current path point to the next path point. This method is same as finding the intersect points of a line and a plane equations. See more details of how to extrude a tube along a path in the pipe generation page and Intersection of Plane and Line page. Or, download the C++ source code of TorusKnot class.
With various pairs of (p, q) combinations, you can create various shapes of torus knots. If q is 0, then the shape is same as torus.






























struct vec3
{
float x;
float y;
float z;
}
// generate path of torus knot with (sectorCount+1) points
// x = (R + r * cos(q*u)) * cos(p*u)
// y = (R + r * cos(q*u)) * sin(p*u)
// z = r * sin(q*u)
void TorusKnot::buildPath()
{
const float PI = acos(-1.0f);
vec3 v;
float sectorStep = 2 * PI / sectorCount;
for(int i = 0; i <= sectorCount; ++i)
{
float angle = i * sectorStep; // starting from 0 to 2pi
float xy = minorRadius * cosf(q*angle); // r * cos(qu)
v.z = minorRadius * sinf(q * angle); // r * sin(qu)
v.x = (majorRadius + xy) * cosf(p * angle);
v.y = (majorRadius + xy) * sinf(p * angle);
path.push_back(v);
}
}
// generate circle on XY plane with tube radius
// x = r * cos(v)
// y = r * sin(v)
// z = 0
void TorusKnot::buildContour()
{
const float PI = acos(-1.0f);
vec3 v;
float sideStep = 2 * PI / sideCount;
v.z = 0;
for(int i = 0; i <= sideCount; ++i)
{
float angle = i * sideStep;
v.x = tubeRadius * cosf(angle);
v.y = tubeRadius * sinf(angle);
contour.push_back(v); // first contour
}
}
Example: Torus Knot
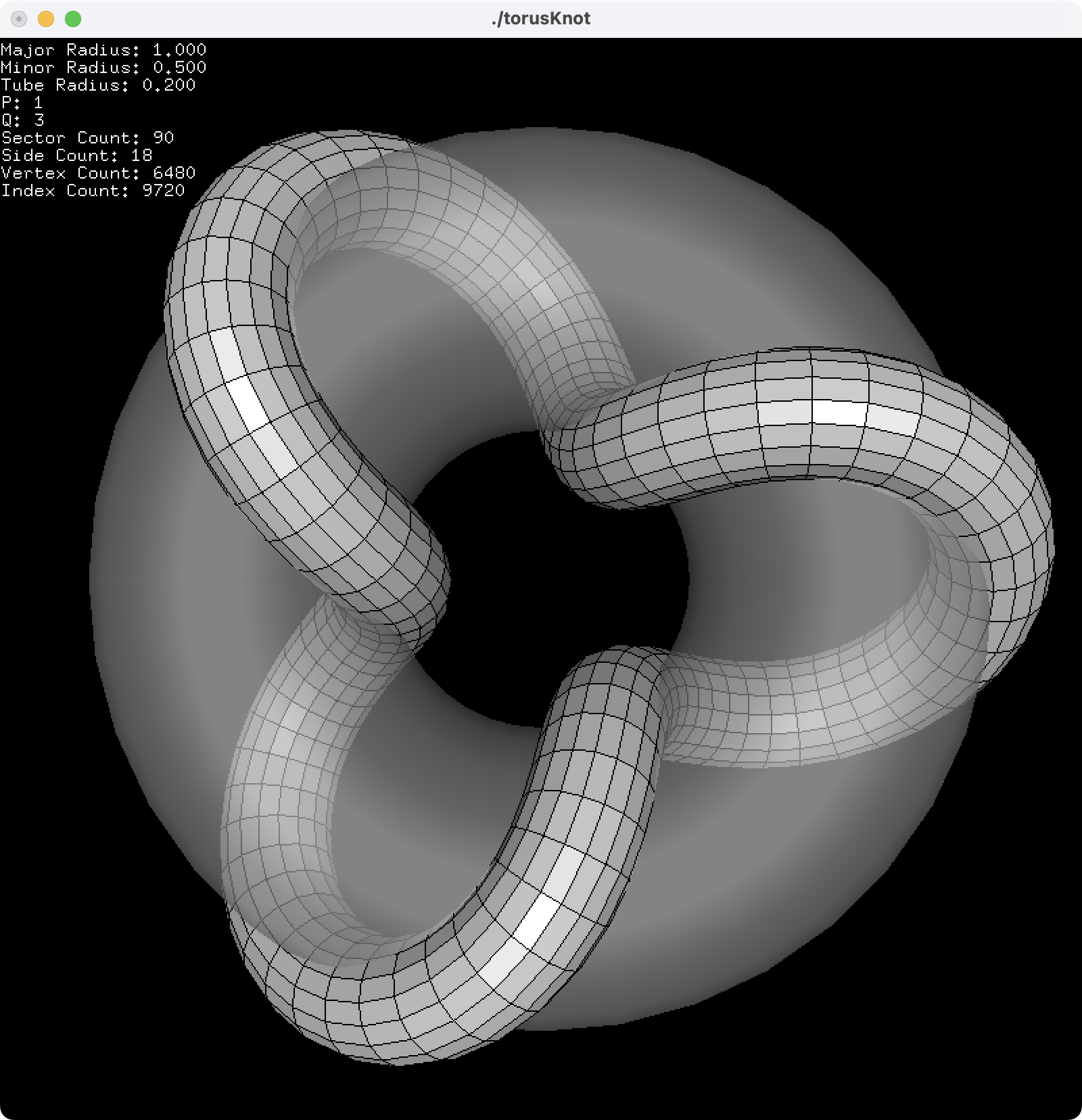

Download: torusKnot.zip (with freeglut), torusKnotShader.zip (with GLFW) (Updated 2025-10-23)
This C++ example constructs a torus knot with given parameters. The default parameters are major radius 1, minor radius 0.5, tube radius 0.2, p=1, q=3, 90 sectors and 18 sides and smooth shading. Use p key to change the number of p windings, and press q to modify the number of q windings. And press the space key to toggle the texture map.
Same as Torus.cpp class, it provides pre-defined drawing functions; draw(), drawWithLines(), drawPath(), and drawLines(), to draw a torus knot using OpenGL VertexArray.
This C++ class also provides getVertices(), getIndices(), getInterleavedVertices(), etc. in order to access the vertex data in GLSL shaders. See the details in torusKnotShader.zip.
// create a torus knot with
// R=1, r=0.5, t=0.2, p=1, q=3, sectors=90, stacks=18, smooth=true, up=Z
TorusKnot knot();
TorusKnot knot(1.0f, 0.5f, 0.2f, 1, 3, 90, 18, true, 3); // same as above
// you can change parameters later
knot.setMajorRadius(2.0f);
knot.setMinorRadius(1.0f);
knot.setTubeRadius(0.5f);
knot.setP(3);
knot.setP(5);
knot.setSectorCount(180);
knot.setSideCount(4);
knot.setSmooth(false);
knot.setUpAxis(2) // X=1, Y=2, Z=3
...
// draw torus knot using vertexarray
knot.draw();
knot.drawWithLines(); // draw torus knot with lines
knot.drawPath(); // draw path line only
Example: WebGL Torus Knot
This example is to draw a torus knot using WebGL. It is a JavaScript version of TorusKnot class. You can download TorusKnot.js from GitHub repo. The fullscreen demo is available at test_torusKnot.html.
// create a torus knot
let knot = new TorusKnot();
// you can change parameters later
knot.setMajorRadius(2.0f);
knot.setMinorRadius(1.0f);
knot.setTubeRadius(0.5f);
knot.setP(3);
knot.setP(5);
...
// draw torus knot with interleaved mode
gl.bindBuffer(gl.ARRAY_BUFFER, knot.vboVertex);
gl.vertexAttribPointer(gl.program.attribPosition, 3, gl.FLOAT, false, knot.stride, 0);
gl.vertexAttribPointer(gl.program.attribNormal, 3, gl.FLOAT, false, knot.stride, 12);
gl.vertexAttribPointer(gl.program.attribTexCoord0, 2, gl.FLOAT, false, knot.stride, 24);
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, knot.vboIndex);
gl.drawElements(gl.TRIANGLES, knot.getIndexCount(), gl.UNSIGNED_SHORT, 0);
...
Trefoil Knot

A trefoil knot is a simplest knot with 3 crossings, and it is shaped like a 3-leaf clover. It is similar to a (2, 3)-torus knot, but it does not perfectly fit on a torus.
The parametric equation of the path of a trefoil knot is:
where R is the major radius, r is the minor radius of the torus.
The parametric equation can be generalized for N-leaf trefoil knots, where n is the the number of leaves; 2, 3, 4, and so on.
Here are various shapes of N-leaf trefoil knots.
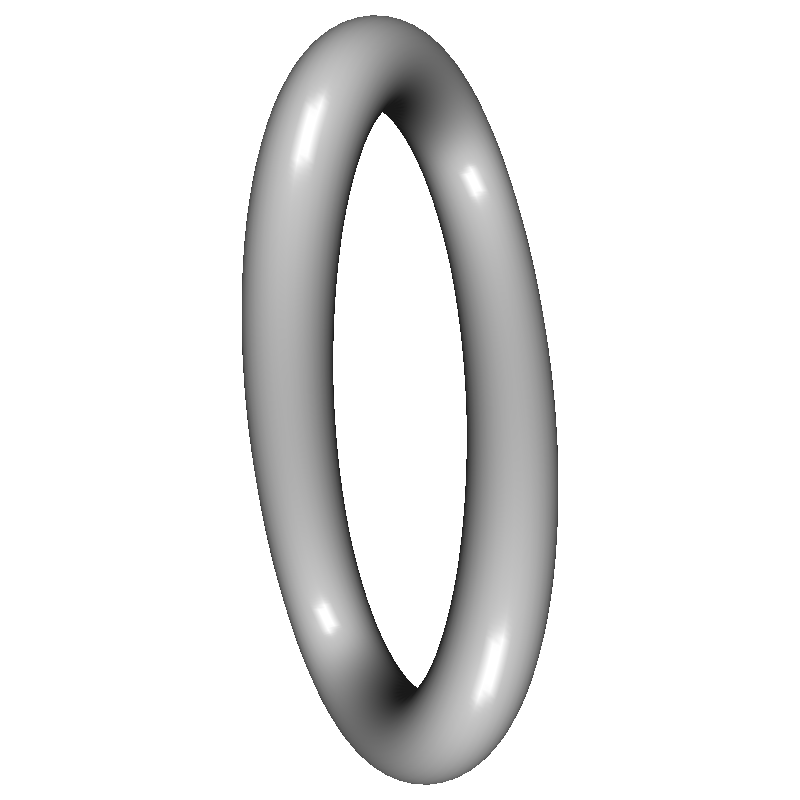

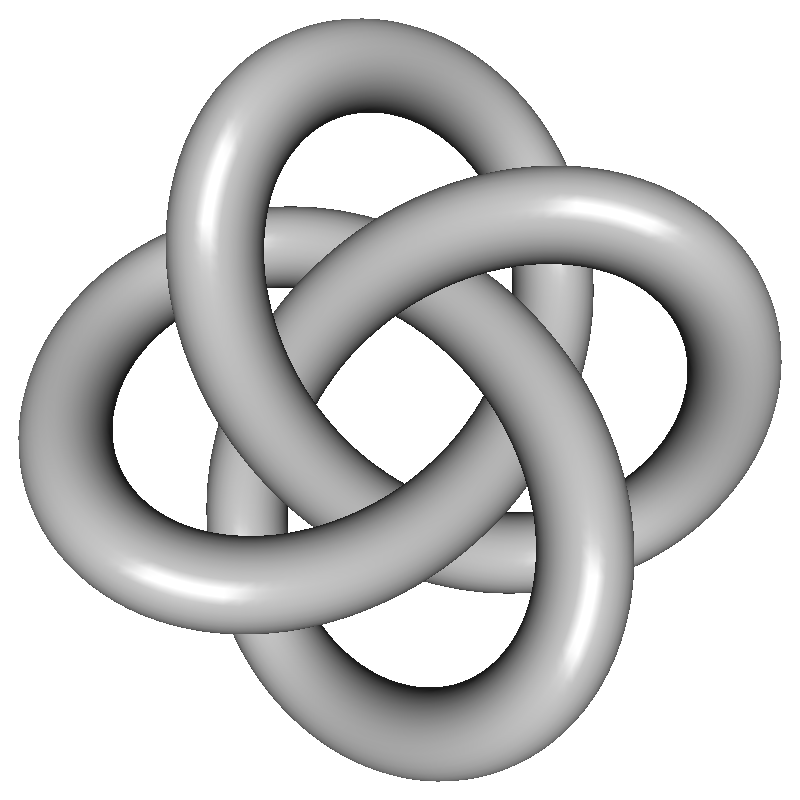




Once you find the path of the trefoil knot, we simply draw a tube following the path to construct a 3D geometry of the trefoil knot. See the detail implementations in buildVerticesSmooth() and buildVerticesFlat() of TrefoilKnot.cpp class.
struct vec3
{
float x;
float y;
float z;
}
// generate path of trefoil knot with (sectorCount+1) points
// x = r * sin(a) - R * sin((N-1)*a)
// y = r * cos(a) + R * cos((N-1)*a)
// z = r * sin(N*a)
void TrefoilKnot::buildPath()
{
vec3 v;
float a; // angle
float sectorStep = 2 * PI / sectorCount;
for(int i = 0; i <= sectorCount; ++i)
{
a = i * sectorStep; // starting from 0 to 2pi
v.x = r * sinf(a) - R * sinf((n-1)*a);
v.y = r * cosf(a) + R * cosf((n-1)*a);
v.z = r * sinf(n*a);
path.push_back(v);
}
}
// build vertices of trefoil knot with smooth shading
void TrefoilKnot::buildVerticesSmooth()
{
this->buildPath();
// add first contour
this->transformFirstContour();
std::vector<vec3> circle = contour;
vec3 p = path[0];
for(int i = 0; i <= sideCount; ++i)
{
vec3 c = circle[i];
vec3 n = (c - p).normalize();
addVertex(c.x, c.y, c.z);
addNormal(n.x, n.y, n.z);
}
// add rest of contours
for(int i = 0; i < sectorCount; ++i)
{
vec3 p = path[i+1];
circle = projectContour(circle, i, i+1);
for(int j = 0; j <= sideCount; ++j)
{
vec3 c = circle[j];
vec3 n = (c - p).normalize();
addVertex(c.x, c.y, c.z);
addNormal(n.x, n.y, n.z);
}
}
// build indices
// k1--k2
// | / |
// | / |
// k1+1-k2+1
unsigned int k1, k2;
for(int i = 0; i < sectorCount; ++i)
{
k1 = i * (sideCount + 1); // beginning of current sector
k2 = k1 + sideCount + 1; // beginning of next sector
for(int j = 0; j < sideCount; ++j, ++k1, ++k2)
{
// 2 triangles per sector
addIndices(k1, k1+1, k2); // k1---k+1---k2
addIndices(k2, k1+1, k2+1); // k2---k1+1--k2+1
}
}
}
Example: Trefoil Knot (C++)
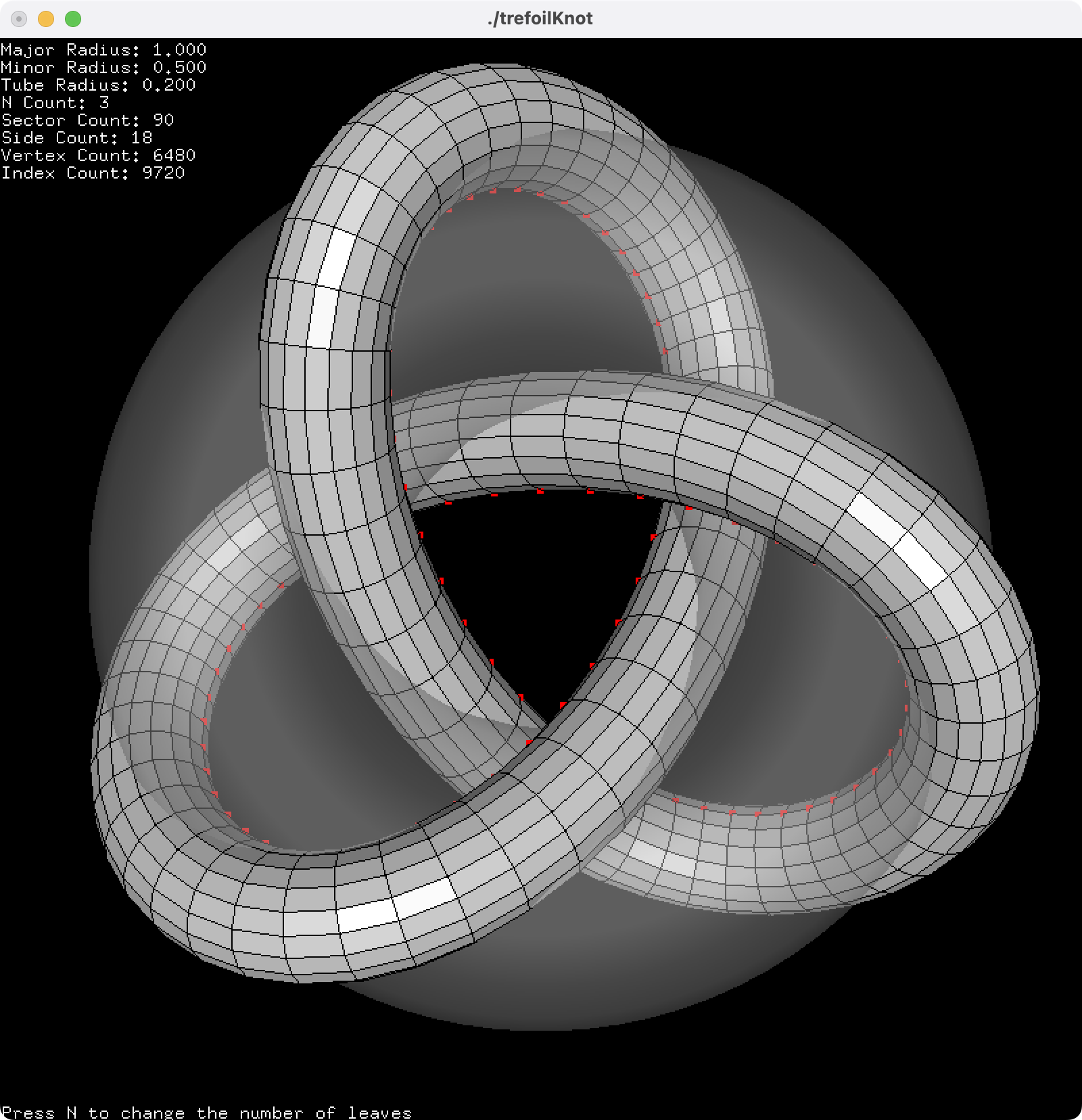
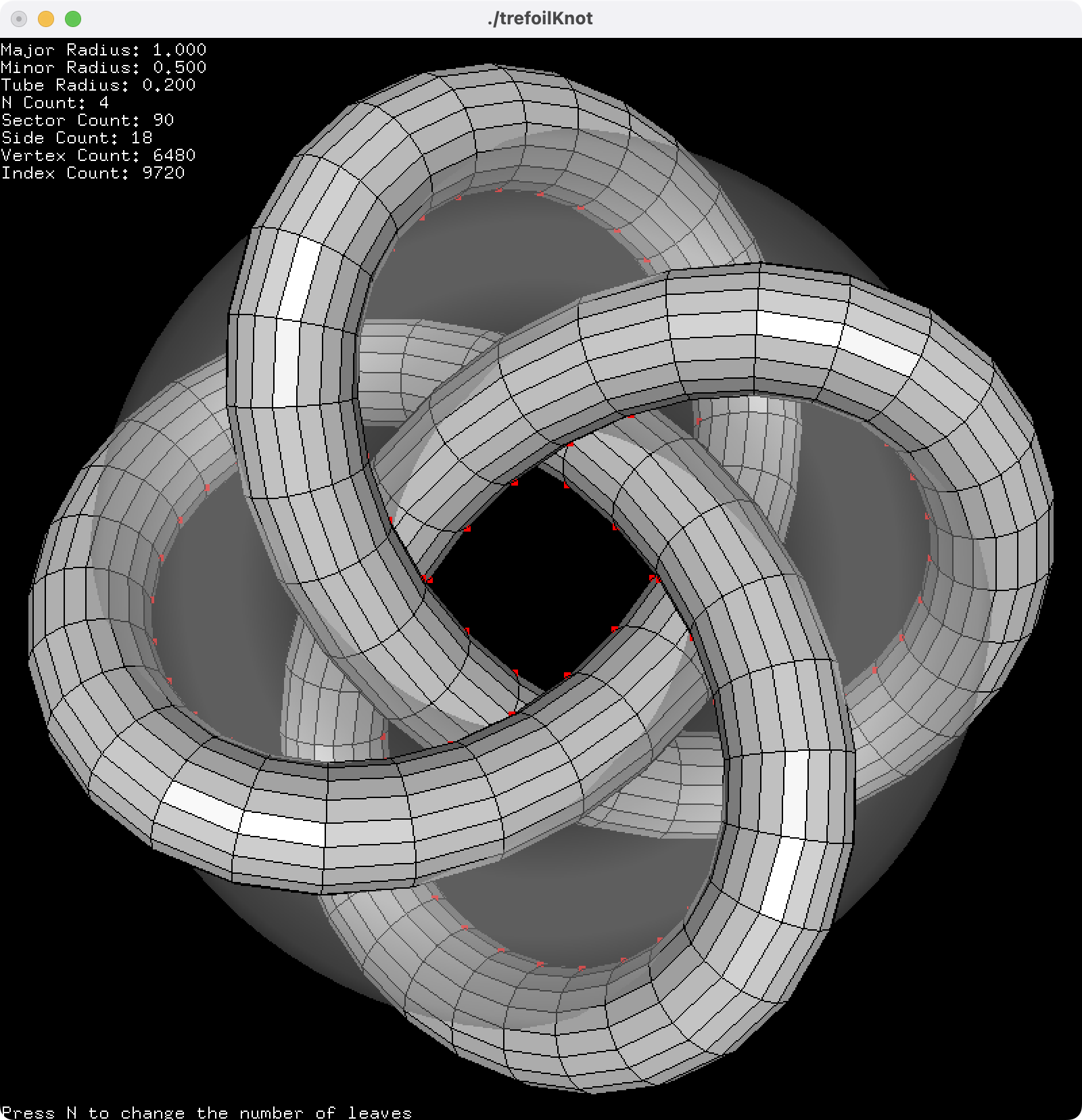
Download: trefoilKnot.zip (with freeglut), trefoilKnotShader.zip (with GLFW) (Updated 2026-02-04)
This C++ example constructs a N-leaf trefoil knot with given parameters. The default parameters are major radius 1, minor radius 0.5, tube radius 0.2, N=3, 90 sectors and 18 sides and smooth shading. Use N key to change the number of leaves. And press the space key to toggle the texture map.
Same as TorusKnot.cpp class, it provides pre-defined drawing functions; draw(), drawWithLines(), drawPath(), and drawLines(), to draw a trefoil knot using OpenGL VertexArray.
This C++ class also provides getVertices(), getIndices(), getInterleavedVertices(), etc. in order to access the vertex data in GLSL shaders. See the details in trefoilKnotShader.zip.
// create a trefoil knot with
// R=1, r=0.5, t=0.2, n=3, sectors=90, stacks=18, smooth=true, up=Z
TrefoilKnot knot();
TrefoilKnot knot(1.0f, 0.5f, 0.2f, 3, 90, 18, true, 3); // same as above
// you can change parameters later
knot.setMajorRadius(2.0f);
knot.setMinorRadius(1.0f);
knot.setTubeRadius(0.5f);
knot.setN(4);
knot.setSectorCount(180);
knot.setSideCount(4);
knot.setSmooth(false);
knot.setUpAxis(2) // X=1, Y=2, Z=3
...
// draw trefoil knot using vertexarray
knot.draw();
knot.drawWithLines(); // draw trefoil knot with lines
knot.drawPath(); // draw path line only
Example: WebGL Trefoil Knot (JS)
This example is to draw a trefoil knot using WebGL. It is a JavaScript version of TrefoilKnot class. You can download TrefoilKnot.js from GitHub repo. The fullscreen demo is available at test_trefoilKnot.html.
// create a trefoil knot
let knot = new TrefoilKnot();
// you can change parameters later
knot.setMajorRadius(2.0f);
knot.setMinorRadius(1.0f);
knot.setTubeRadius(0.5f);
knot.setN(5);
...
// draw trefoil knot with interleaved mode
gl.bindBuffer(gl.ARRAY_BUFFER, knot.vboVertex);
gl.vertexAttribPointer(gl.program.attribPosition, 3, gl.FLOAT, false, knot.stride, 0);
gl.vertexAttribPointer(gl.program.attribNormal, 3, gl.FLOAT, false, knot.stride, 12);
gl.vertexAttribPointer(gl.program.attribTexCoord0, 2, gl.FLOAT, false, knot.stride, 24);
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, knot.vboIndex);
gl.drawElements(gl.TRIANGLES, knot.getIndexCount(), gl.UNSIGNED_SHORT, 0);
...