WebGL: Gaussian Blur

←Back

Related Topics: Convolution, Render To Texture, Image

Overview

gaussian blur
Gaussian Blur at the standard deviation, σ = 0, 1, 2, 3 respectively
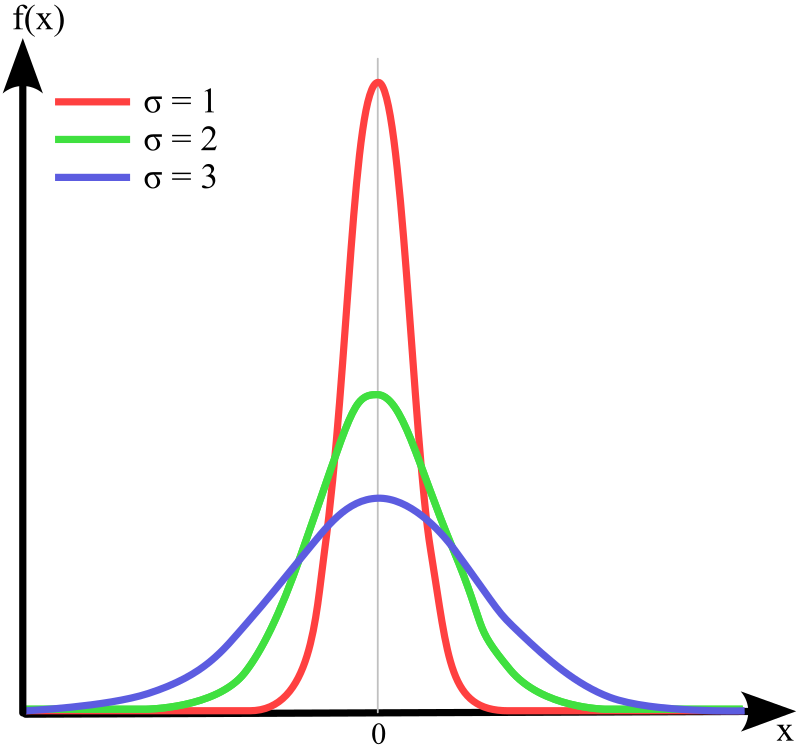
gaussian function
Gaussian Function

Gaussian function (or normal distribution function) is widely used in various areas. The standard deviation, σ determines how wide the data spead out around the mean value. A greater standard deviation disperses the data wider.
gaussian function

In image processing, Gaussian function is used to smooth or blur the input image or remove noise from the source image by 2D convolution with the input image and Gaussian filter (kernel).

In computer graphics, Gaussian blur is used to soften the hard edges of the shadow map or to create bloom effects.

This page explains how to perform Gaussian blur in WebGL using GLSL shaders, and some performance optimizations.

Generate Gaussian Kernel

In general, 2D convolution requires a 2D kernel (filter). But, it can be optimized by performing 1D convolution twice with a 1D kernel, if the kernel is separable. (2D convolution with MxN kernel requires MxN multiplications, but 1D convolution with Mx1 and 1xN seperable kernels only requires M+N multiplications.)

Gaussian filter is a symmetric function on both vertical/horizontal directions, so it is a seperable kernel. Therefore, Gaussian blur can be optimized by performing 1D convolution along vertical and horizontal directions, instead of 2D convolution.

The following function is to generate 1D Gaussian kernel with the given standard deviation and kernel size. If the standard deviation σ is greater, it also requires the larger kernel size. Note that the sum of all kernel elements should be 1 for low-pass filters, so the values are normalized. Please see convolutionUtils.js for more details. 


// generate 1D seperable gaussian kernel
function generateGaussianKernel(sigma, kernelSize)
{
    let kernel = new Float32Array(kernelSize);

    // compute kernel elements of Gaussian
    // do only half(positive side) and mirror to negative side
    // because Gaussian is even function, symmetric to Y-axis.
    let center = Math.floor(kernelSize / 2);   // center value of n-array(0 ~ n-1)

    let result = 0;
    let sum = 0;
    if(sigma == 0)
    {
        kernel.fill(0);
        kernel[center] = 1.0;
    }
    else
    {
        const SS2 = sigma * sigma * 2;
        kernel[center] = 1;
        sum = 1;
        for(let x = 1; x <= center; ++x)
        {
            // dividing (sqrt(2*PI)*sigma) is not needed because normalizing result later
            result = Math.exp(-(x*x)/SS2);
            kernel[center+x] = kernel[center-x] = result;
            sum += result;
            sum += result;
        }

        // normalize kernel
        // make sum of all elements in kernel to 1
        for(let i = 0; i <= center; ++i)
            kernel[center+i] = kernel[center-i] /= sum;
    }
    return kernel;
}
...

// create 1D gaussian kernel with sigma=3 and kernel size=15
let kernel = createGaussianKernel(3, 15);

Since the Gaussian kernel is symmetric along Y-axis (even function), we can reduce the array size to store the kernel values only on the positive side including the center value. Then, mirror the values for the negative Y-axis side. 


// generate half size 1D seperable gaussian kernel
function generateHalfGaussianKernel(sigma, halfKernelSize)
{
    let kernel = new Float32Array(halfKernelSize);
    let result = 0;
    let sum = 0;
    if(sigma == 0)
    {
        kernel.fill(0);
        kernel[0] = 1.0;
    }
    else
    {
        const SS2 = sigma * sigma * 2;
        kernel[0] = 1;
        sum = 1;
        for(let x = 1; x < halfKernelSize; ++x)
        {
            result = Math.exp(-(x*x)/SS2);
            kernel[x] = result;
            sum += result * 2;
        }

        // normalize kernel
        for(let i = 0; i <= halfKernelSize; ++i)
            kernel[i] /= sum;
    }
    return kernel;

Shader for Gaussian Blur

Once you generate a half Gaussian kernel, you can pass the array to a GLSL shader as a uniform value. Note that the array size of a uniform in GLSL cannot be changed. So, you need to define a uniform array with a fixed size in the shader. If the actual kernel size is smaller than the uniform array, then, pad zeros for the unused array elements.

The formula of 1D convolution is;
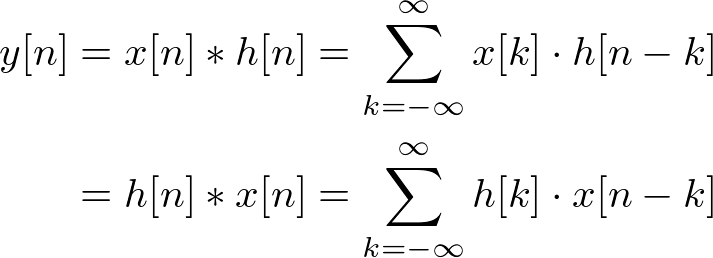
1D convolution
where x[n] is the input image and h[n] is the kernel.

For example, the output at y[3] can be computed as
1D convolution example

The following is GLSL shaders and JavaScript codes to perform 1D convolution with a separable Gaussian kernel. WebGL requires FBO and Quad classes to hold images and to perform render-to-texture. 


// load image
gl.tex0 = loadTexture(gl, "lena_color_512.jpg", false);

// create quad to draw image
gl.quad = new Quad(gl, 0, 512, 0, 512); // l,r,b,t
gl.quad.reverseTextureOrientation();    // swap orientation

// create fbos for image processing
gl.fbo1 = new FrameBuffer(gl);
gl.fbo2 = new FrameBuffer(gl);
gl.fbo1.init(512, 512);
gl.fbo2.init(512, 512);

// generate half gaussian kernel with sigma=3, size=11
gl.kernel = generateHalfGaussianKernel(3, 11);
gl.kernel = resizeHalfKernel(gl.kernel, 21); // pad 0s for unused elemets
...

// blur image with 1D convolution both direction
blurImage(gl.tex0, gl.fbo1, new Vector2(1,0));      // horizontal
blurImage(gl.fbo1.tex, gl.fbo2, new Vector2(0,1));  // vertical

// render to texture (fbo)
function blurImage(texId, fbo, direction)
{
    gl.program = gl.shaderPrograms["gaussian"];
    if(!gl.program) return;
    gl.useProgram(gl.program);

    fbo.bind();

    gl.viewport(0, 0, fbo.width, fbo.height);
    gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

    // pass uniforms
    gl.uniform1fv(gl.program.uniform.kernel, gl.kernel);
    gl.uniform2f(gl.program.uniform.screenDimension, fbo.width, fbo.height);
    gl.uniform2f(gl.program.uniform.direction, direction.x, direction.y);
    if(direction.x == 0)
        gl.uniform1f(gl.program.uniform.imageDimension, fbo.height);
    else
        gl.uniform1f(gl.program.uniform.imageDimension, fbo.width);

    gl.activeTexture(gl.TEXTURE0);
    gl.bindTexture(gl.TEXTURE_2D, texId);
    gl.quad.draw();

    fbo.unbind();
}



// Gaussian Blur vertex shader
// constants
const float ZERO = 0.0;
const float ONE  = 1.0;

// vertex attributes
attribute vec2 vertexPosition;      // 2D position
attribute vec2 vertexTexCoord0;

// uniforms
uniform vec2 screenDimension;

// output varying variables
varying vec2 texCoord0;

void main(void)
{
    texCoord0 = vertexTexCoord0;

    // normalized position [-1, 1]
    vec2 normPosition = (vertexPosition / screenDimension) * TWO - ONE;
    gl_Position = vec4(normPosition, ZERO, ONE);
}



// Gaussian Blur Fragment Shader
// constants
const int MAX_KERNEL = 21;              // max half kernel size including the center
const float ZERO = 0.0;
const float ONE  = 1.0;

// uniforms
uniform float kernel[MAX_KERNEL];       // half gaussian kernel from center
uniform float imageDimension;
uniform vec2 direction;                 // horizontal=(1,0) or vertical=(0,1)
uniform sampler2D map0;                 // input image

// input varying variables
varying vec2 texCoord0;

void main(void)
{
    // compute the center first
    vec3 color = texture2D(map0, texCoord0).rgb * kernel[0];
    vec2 offset;

    // compute with other kernel elements
    for(int i = 1; i < MAX_KERNEL; ++i)
    {
        offset = direction * float(i) / imageDimension;
        color += texture2D(map0, texCoord0 + offset).rgb * kernel[i]; // positive side
        color += texture2D(map0, texCoord0 - offset).rgb * kernel[i]; // negative side
    }

    gl_FragColor = vec4(color, ONE);
}

Optimization with Texture Filtering

The convolution in GLSL shaders can be further optimized by GPU's texture linear filtering. The previous convolution takes N multiplications by texture samples with Nx1 kernel, where Pi is a texel and Hi is a kernel value.
convolve

We can use the linearly interpolated value between 2 texels instead, so we only need to multiply a half number of samples. For example, WebGL texture filtering interpolates the texture sample P1 and P2 and returns P1-2;
interpolate

Therefore, the weighted sum of 2 samples, P1H1 + P2H2 can be reduced to P1-2H.
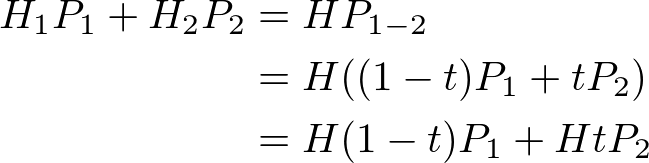
interpolate 2

To use the interpolated texel, we need to find a new interpolated kernel value H and the interpolation amount, t from the above equations.
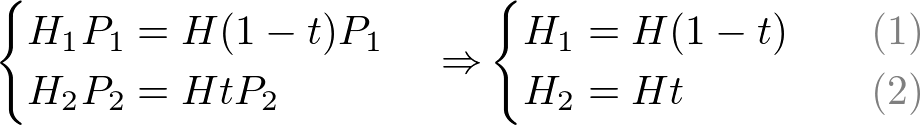
interpolate 3

From the equation (2), we can find t first;
interpolate 4

Then, we can determine H is H1 + H2 by substituting t into the equation (1);
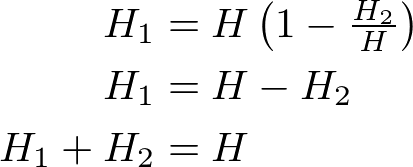
interpolate 5

Here is the optimized GLSL fragment shader using the texture filtering. Or, you can download it from GitHub Repo. 


// Gaussian Blur Fragment Shader with texture filtering
// constants
const int MAX_KERNEL = 21;              // max half kernel size including the center
const float ZERO = 0.0;
const float ONE  = 1.0;

// uniforms
uniform float kernel[MAX_KERNEL];       // half gaussian kernel from center
uniform float imageDimension;
uniform vec2 direction;                 // horizontal=(1,0) or vertical=(0,1)
uniform sampler2D map0;                 // input image

// input varying variables
varying vec2 texCoord0;

void main(void)
{
    // compute the center texel first
    vec3 color = texture2D(map0, texCoord0).rgb * kernel[0];
    vec2 offset;

    // optimize using linear texture filtering (with half texels)
    float k;    // interpolated kernel
    float t;    // interpolated alpha
    for(int i = 1; i < MAX_KERNEL; i += 2)
    {
        k = kernel[i] + kernel[i+1];
        t = kernel[i+1] / k;
        offset = direction * (float(i) + t) / imageDimension;
        color += texture2D(map0, texCoord0 + offset).rgb * k;
        color += texture2D(map0, texCoord0 - offset).rgb * k;
    }

    gl_FragColor = vec4(color, ONE);
}

Example

This example performs convolution with a Gaussian kernel to blur the image. You can slide the standard deviation value to change the gaussian filter.


decoration Fullscreen Demo: test_blur.html
decoration GitHub Repo: test_blur.html

←Back
 
Hide Comments
comments powered by Disqus