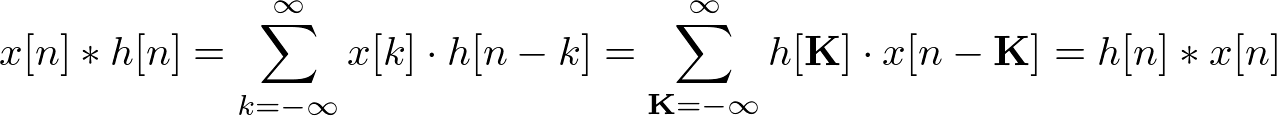Proof of Commutative Property of Convolution

The definition of convolution 1D is:

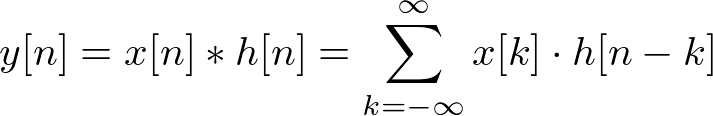
First, let

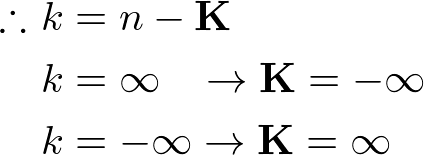
Then, substitute K into the equation:

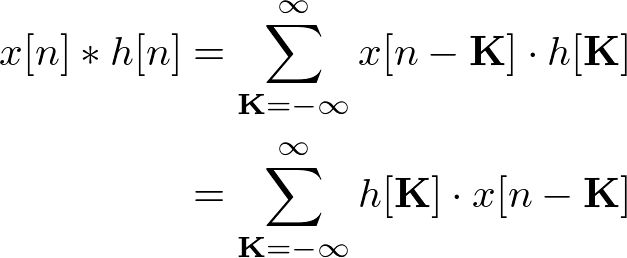
By definition, 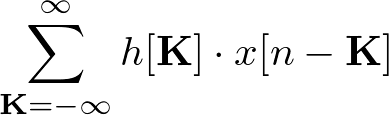is the convolution of two signals h[n] and x[n], which is .

Therefore, convolution is commutative; .