OpenGL Camera

Related Topics: OpenGL Transform, OpenGL Projection Matrix, Quaternion to Rotation Matrix
Download: OrbitCamera.zip, trackball.zip, cameraRotate.zip, cameraShift.zip

• Overview
• Camera LookAt
• Camera Rotation (Pitch, Yaw, Roll)
• Camera Shifting and Forwarding
• Example: Orbit Camera
• Example: Trackball

Overview

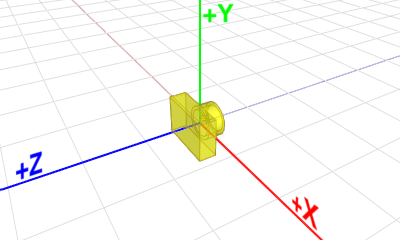
OpenGL doesn't explicitly define neither camera object nor a specific matrix for camera transformation. Instead, OpenGL transforms the entire scene (including the camera) inversely to a space, where a fixed camera is at the origin (0,0,0) and always looking along -Z axis. This space is called eye space.

Because of this, OpenGL uses a single GL_MODELVIEW matrix for both object transformation to world space and camera (view) transformation to eye space.

You may break it down into 2 logical sub matrices;

That is, each object in a scene is transformed with its own M_model first, then the entire scene is transformed reversely with M_view. In this page, we will discuss only M_view for camera transformation in OpenGL.

LookAt

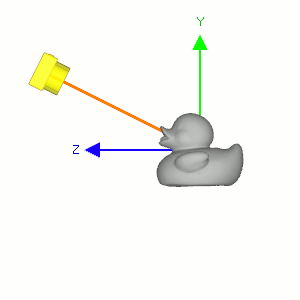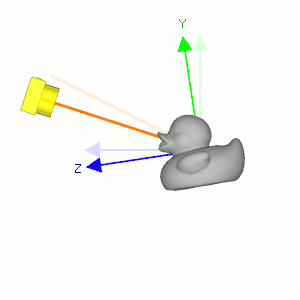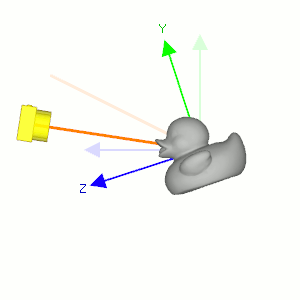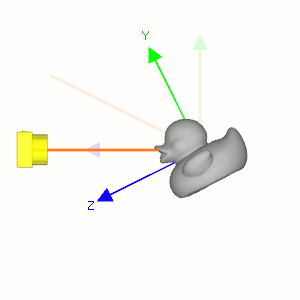
gluLookAt() is used to construct a viewing matrix where a camera is located at the eye position and looking at (or rotating to) the target point . The eye position and target are defined in world space. This section describes how to implement the viewing matrix equivalent to gluLookAt().

Camera's lookAt transformation consists of 2 transformations; translating the whole scene inversely from the eye position to the origin (M_T), and then rotating the scene with reverse orientation (M_R), so the camera is positioned at the origin and facing to the -Z axis.

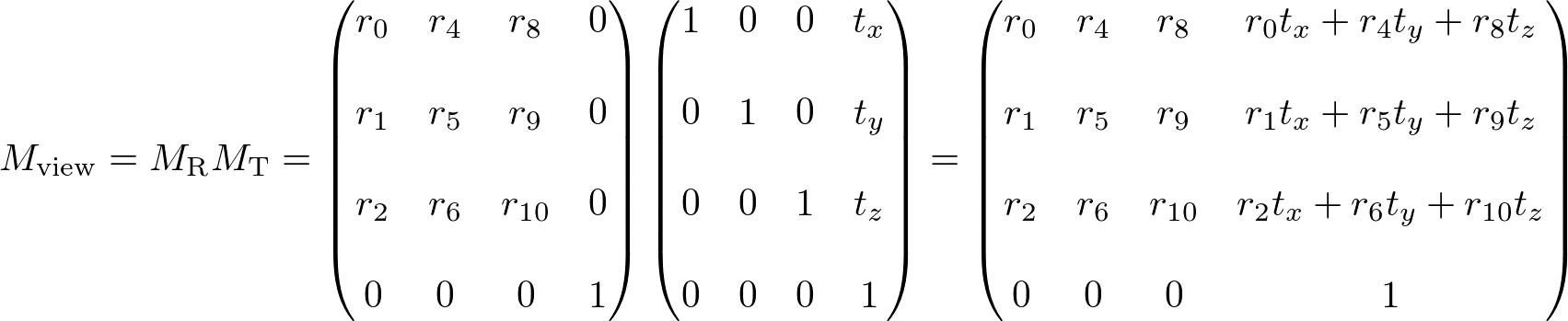
Suppose a camera is located at (2, 0, 3) and looking at (0, 0, 0) in world space. In order to construct the viewing matrix for this case, we need to translate the world to (-2, 0, -3) and rotate it about -33.7 degree along Y-axis. As a result, the virtual camera becomes facing to -Z axis at the origin.

The translation part of lookAt is easy. You simply move the camera position to the origin. The translation matrix M_T would be (replacing the 4th coloumn with the negated eye position);

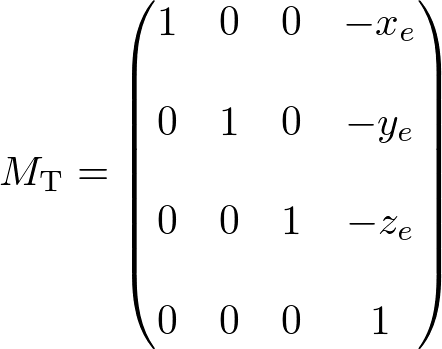
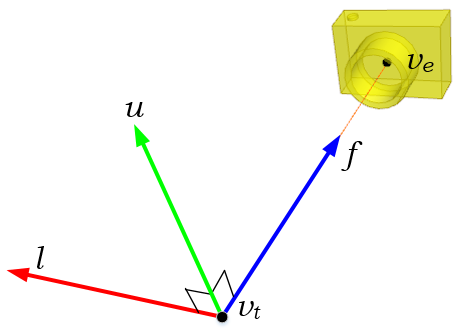
The rotation part M_R of lookAt is much harder than translation because you have to calculate 1st, 2nd and 3rd columns of the rotation matrix all together.

First, compute the normalized forward vector from the target position v_t to the eye position v_e of the rotation matrix. Note that the forward vector is from the target to the eye position, not eye to target because the scene is actually rotated, not the camera is.

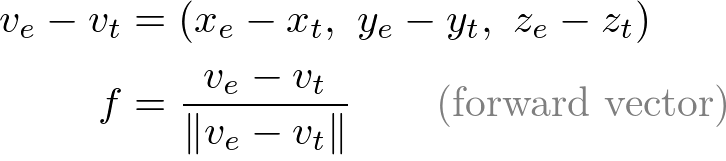
Second, compute the normalized left vector by performing cross product with a given camera's up vector. If the up vector is not provided, you may use (0, 1, 0) by assuming the camera is straight up to +Y axis.

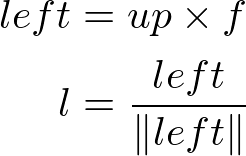
Finally, re-calculate the normalized up vector by doing cross product the forward and left vectors, so all 3 vectors are orthonormal (perpendicular and unit length). Note we do not normalize the up vector because the cross product of 2 perpendicular unit vectors also produces a unit vector.

These 3 basis vectors, , and are used to construct the rotation matrix M_R of lookAt, however, the rotation matrix must be inverted. Suppose a camera is located above a scene. The whole scene must rotate downward inversely, so the camera is facing to -Z axis. In a similar way, if the camera is located at the left of the scene, the scene should rotate to right in order to align the camera to -Z axis. The following diagrams show why the rotation matrix must be inverted.

Therefore, the rotation part M_R of lookAt is finding the rotation matrix from the target to the eye position, then invert it. And, the inverse matrix is equal to its transpose matrix because it is orthogonal which each column has unit length and perpendicular to the other column.

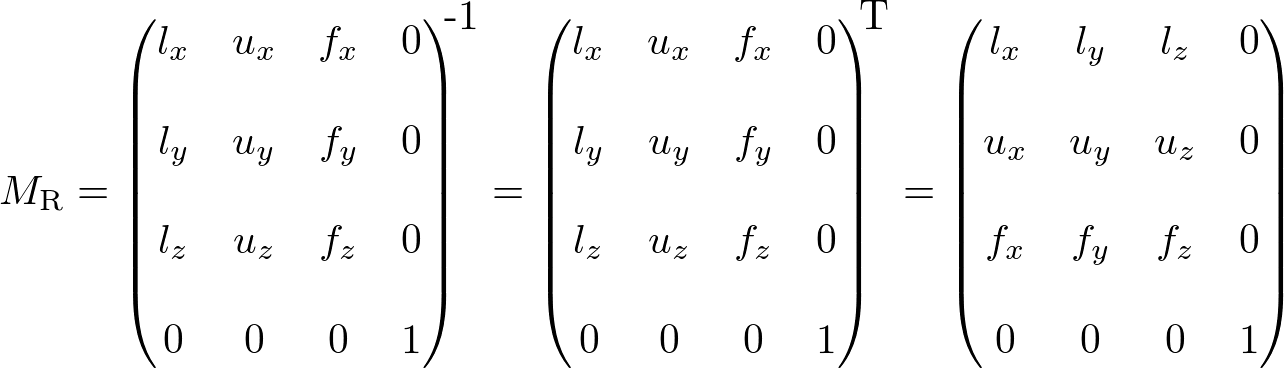
Finally, the view matrix for camera's lookAt transform is multiplying M_T and M_R together;

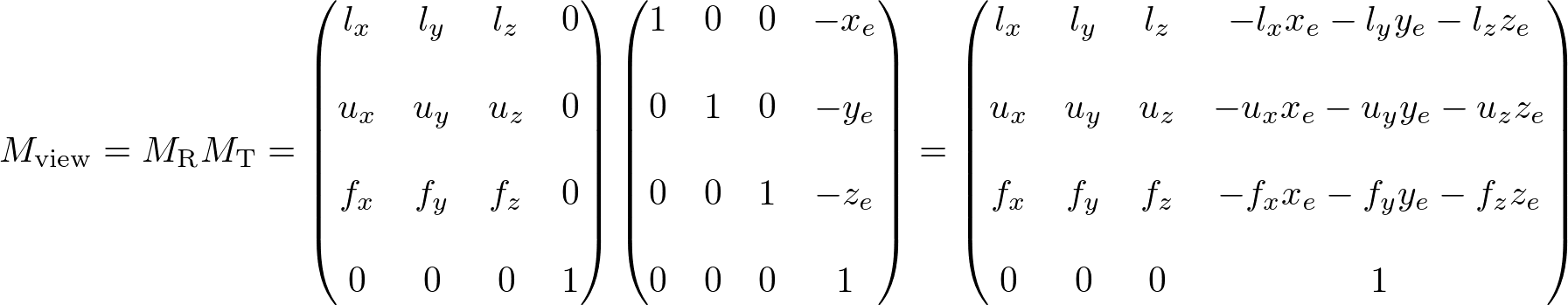
Here is C++ snippet to construct the view matrix for camera's lookAt transformation. Please see the details in OrbitCamera.cpp.

// dependency: Vector3 and Matrix4
struct Vector3
{
    float x;
    float y;
    float z;
};

class Matrix4
{
    float m[16];
}

///////////////////////////////////////////////////////////////////////////////
// equivalent to gluLookAt()
// It returns 4x4 matrix
///////////////////////////////////////////////////////////////////////////////
Matrix4 lookAt(Vector3& eye, Vector3& target, Vector3& upDir)
{
    // compute the forward vector from target to eye
    Vector3 forward = eye - target;
    forward.normalize();                 // make unit length

    // compute the left vector
    Vector3 left = upDir.cross(forward); // cross product
    left.normalize();

    // recompute the orthonormal up vector
    Vector3 up = forward.cross(left);    // cross product

    // init 4x4 matrix
    Matrix4 matrix;
    matrix.identity();

    // set rotation part, inverse rotation matrix: M^-1 = M^T for Euclidean transform
    matrix[0] = left.x;
    matrix[4] = left.y;
    matrix[8] = left.z;
    matrix[1] = up.x;
    matrix[5] = up.y;
    matrix[9] = up.z;
    matrix[2] = forward.x;
    matrix[6] = forward.y;
    matrix[10]= forward.z;

    // set translation part
    matrix[12]= -left.x * eye.x - left.y * eye.y - left.z * eye.z;
    matrix[13]= -up.x * eye.x - up.y * eye.y - up.z * eye.z;
    matrix[14]= -forward.x * eye.x - forward.y * eye.y - forward.z * eye.z;

    return matrix;
}

Camera Rotation (Pitch, Yaw, Roll)

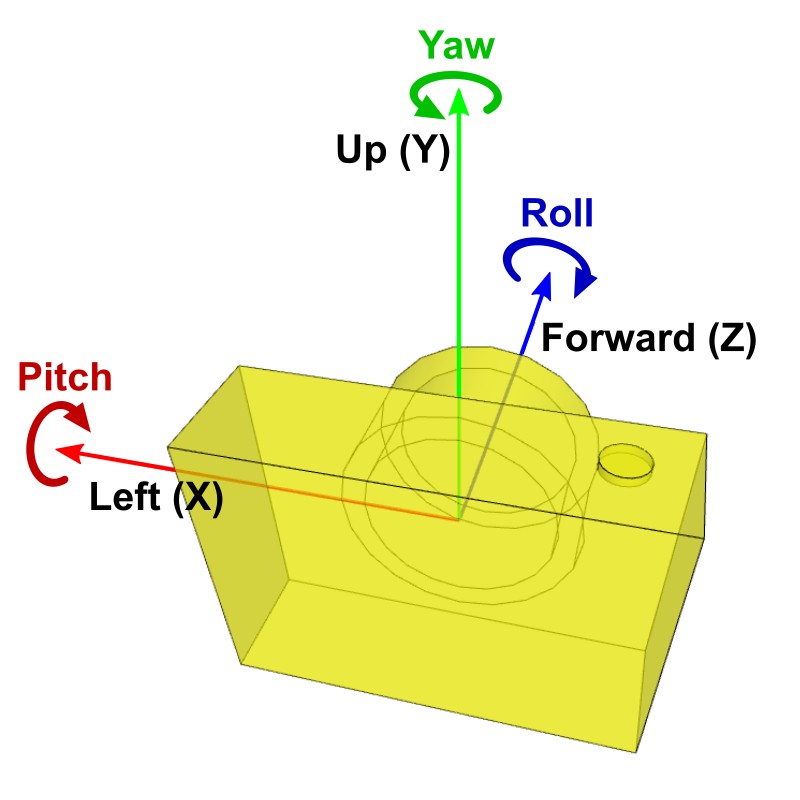
Other types of camera's rotations are pitch, yaw and roll rotating at the position of the camera. Pitch is rotating the camera up and down around the camera's local left axis (+X axis). Yaw is rotating left and right around the camera's local up axis (+Y axis). And, roll is rotating it around the camera's local forward axis (+Z axis).

It is used for a free-look style camera, VR headset movements or first-person shooter camera interface.

First, you need to move the whole scene inversely from the camera's position to the origin (0,0,0), same as lookAt() function. Then, rotate the scene along the rotation axis; pitch (X), yaw (Y) and roll (Z) independently.

If multiple rotations are applied, combine them sequentially. Note that a different order of rotations produces a different result. A commonly used rotation order is roll (Z) → yaw (Y) → pitch (X).

Keep it mind that the directions of the rotations (right-hand rule); a positive pitch angle is rotating the camera downward, a positive yaw angle means rotating the camera left, and a positive roll angle is rotating the camera clockwise.

The following is a C++ code snippet to construct the view matrix for the free-look style camera interface. Notice that only yaw (X) angle is negated but other pitch and roll angles are not. It is because the direction of Y axis on both the virtual camera and view matrix is same, and OpenGL will rotate the whole scene opposite direction. For instance, rotating the camera 30 degree to the left is same as rotating the world 30 degree to the right along Y-axis. However, the pitch (X) and roll (Z) angles are not negated because X and Z axis are already in opposite directions.

// camera position and rotations in world space
Vector3 camPosition = ...;          // (x, y, z)
Vector3 camAngle = ...;             // (pitch, yaw, roll)

// construct view matrix using camera pos and angles (for free-look style)
Matrix4 matrixView;
matrixView.translate(-camPosition); // 1. translate inversely
matrixView.rotateZ(camAngle.z);     // 2. rotate for roll
matrixView.rotateY(-camAngle.y);    // 3. rotate for yaw inversely
matrixView.rotateX(camAngle.x);     // 4. rotate for pitch

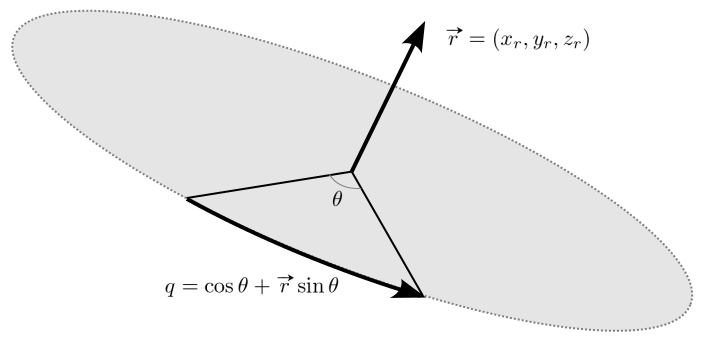
If Quaternion is used for the rotations, the pitch, yaw and roll angles can be converted to the quaternion representations from the rotation axis (X, Y and Z) and the angles amounts.

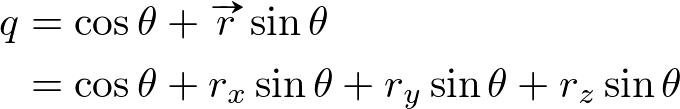
Then, multiply multiple quaternions one after another to construct a sequence of rotations together. Finally, the rotation quaternion is represented as 4x4 matrix form for OpenGL. The conversion is explained at Quaternion to Matrix.

// camera position and rotations in world space
Vector3 camPosition = ...;          // (x, y, z)
Vector3 camAngle = ...;             // (pitch, yaw, roll)

// construct rotation quaternions
Quaternion qx = Quaternion(Vector3(1,0,0), camAngle.x / 2);     // pitch
Quaternion qy = Quaternion(Vector3(0,1,0), -camAngle.y / 2);    // yaw
Quaternion qz = Quaternion(Vector3(0,0,1), camAngle.z / 2);     // roll
Quaternion q = qx * qy * qz;    // rotation order: roll -> yaw -> pitch

// convert quaternion to rotation matrix
Matrix4 matrixRotation = q.getMatrix();

// construct view matrix
matrixView.identity();
matrixView.translate(-camPosition);
matrixView = matrixRotation * matrixView;   // M = Mr * Mt

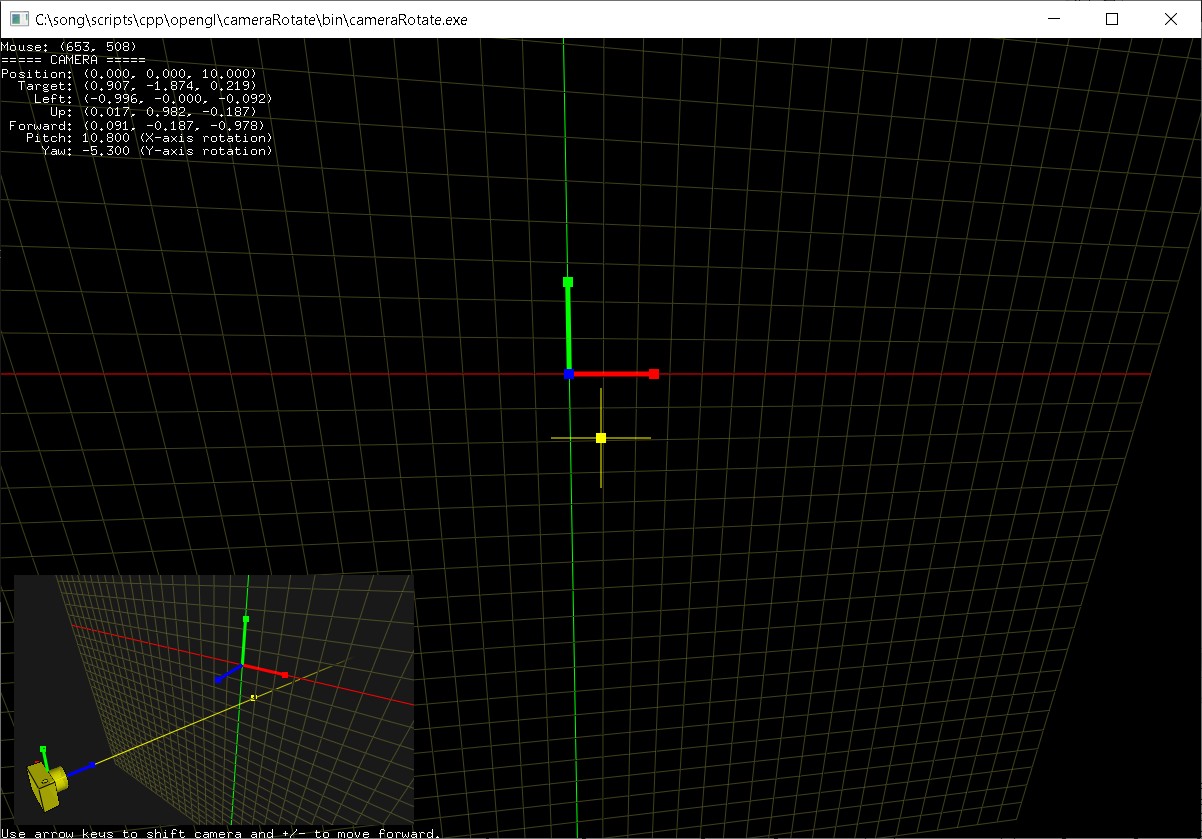
Download cameraRotate.zip and cameraRotateQuaternion.zip to see the complete source code for free-look style camera rotations (pitch, yaw, roll).

Camera Shifting & Forwarding

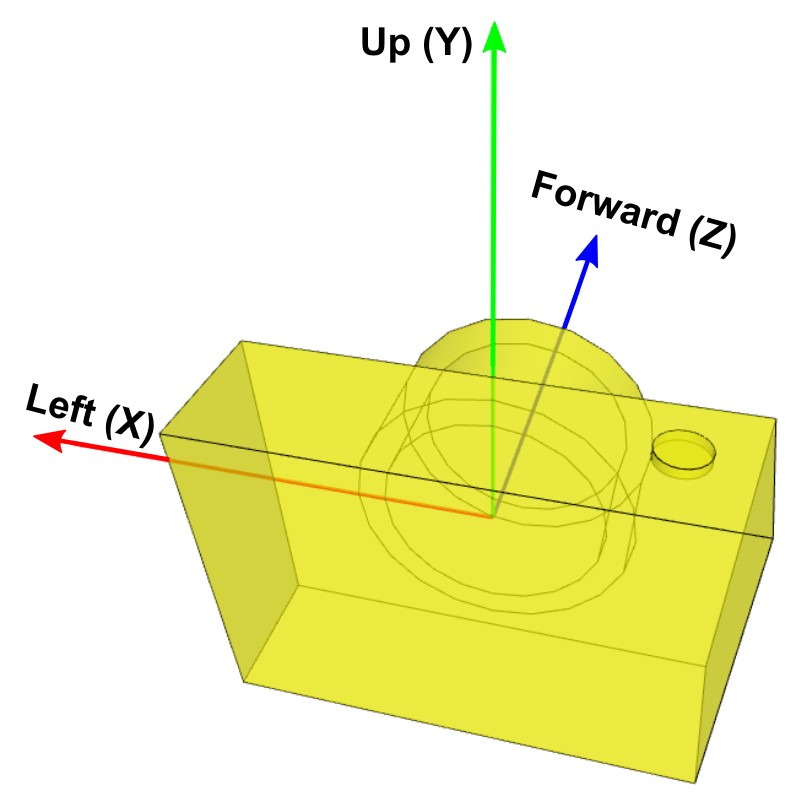
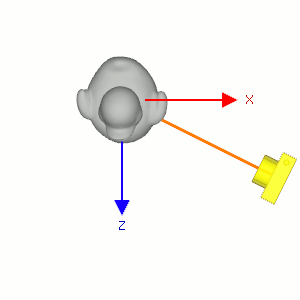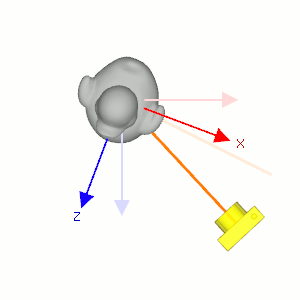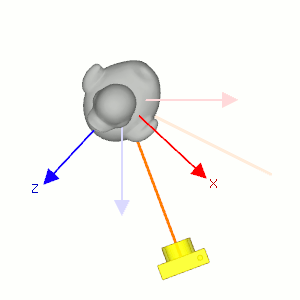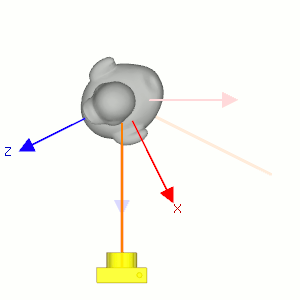
In order to update the camera's position by shifting the camera left and right or up and down, or moving forward and backward, you will need to find 3 local axis vectors of the camera; left, up, and forward vectors at the current position and orientation. These vectors cannot be same as X, Y and Z basis axis of the world space because the virtual camera has been oriented to an arbitary direction. (Moving left/right is not translating along X-axis in the world space.)

If you know the camera position and target points, you can compute the left, up and forward vectors from them by vector subtraction and cross product.

Or, you can also directly get them from the view matrx. The first row of the view matrix is the left vector, the second row is the up vector and the third row is the forward vector.

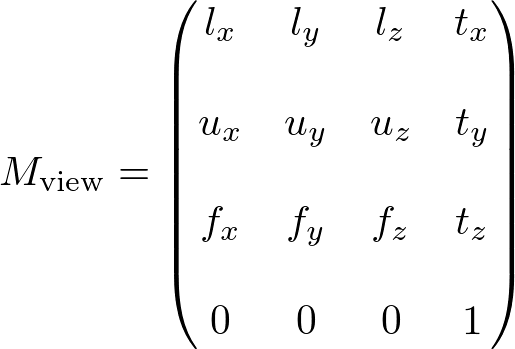
Since the rotation parts of the view matrix are inversely transformed (transposed), these 3 vectors become the row vectors, not column vectors. And, since the X and Z axis of the virual camera are opposite directions, we negate the left and forward vectors. (The Y axis is same in both world space and eye space, so no need to modify the up vector.)

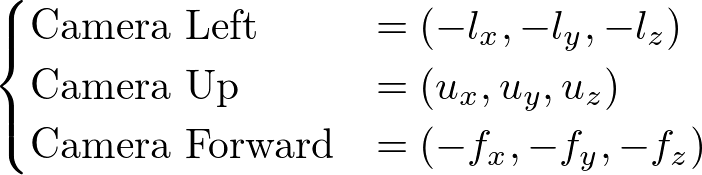
Once we find the left, up and forward vectors, we can finally compute the new camera position in the world space by adding the delta movements along each direction vector. The following code shifting camera horizontal and vertical directions, and moving forward/backward;

Matrix4 matrixView ...;             // current 4x4 view matrix
Vector3 camPosition = ...;          // current pos (x, y, z)
float deltaLeft = ...;              // delta movements
float deltaUp = ...;
float deltaForward = ...;

// left/up/forward vectors are 3 row vectors from the view matrix
//    Left = Vector3(-m[0], -m[4], -m[8])
//      Up = Vector3( m[1],  m[5],  m[9])
// Forward = Vector3(-m[2], -m[6], -m[10])
Vector3 cameraLeft(-matrixView[0], -matrixView[4], -matrixView[8]);
Vector3 cameraUp(matrixView[1], matrixView[5], matrixView[9]);
Vector3 cameraForward(-matrixView[2], -matrixView[6], -matrixView[10]);

// compute delta shift and forward amount
Vector3 deltaMovement = deltaLeft * cameraLeft; // add horizontal
deltaMovement += deltaUp * cameraUp;            // add vertical
deltaMovement += deltaForward * cameraForward;  // add forward

// update new camera's position by adding delta amount
cameraPosition += deltaMovement;

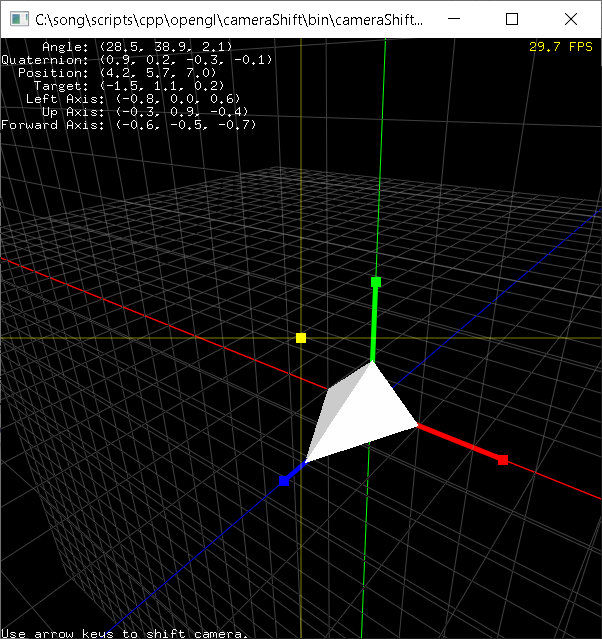
OrbitCamera.cpp class in cameraShift.zip provides various interfaces for the camera movements; moveTo(), shiftTo() and moveForward() to translate the virtual camera to any direction. For continuous animations, use startShift()/stopShift() and startForward()/stopForward().

Use the left/right arrow keys to shift the camera horizontally, and press up/down arrow keys to move the camera vertically. And press +/- keys to move the camera forward or backward.

Download: cameraShift.zip

Example: OpenGL Orbit Camera

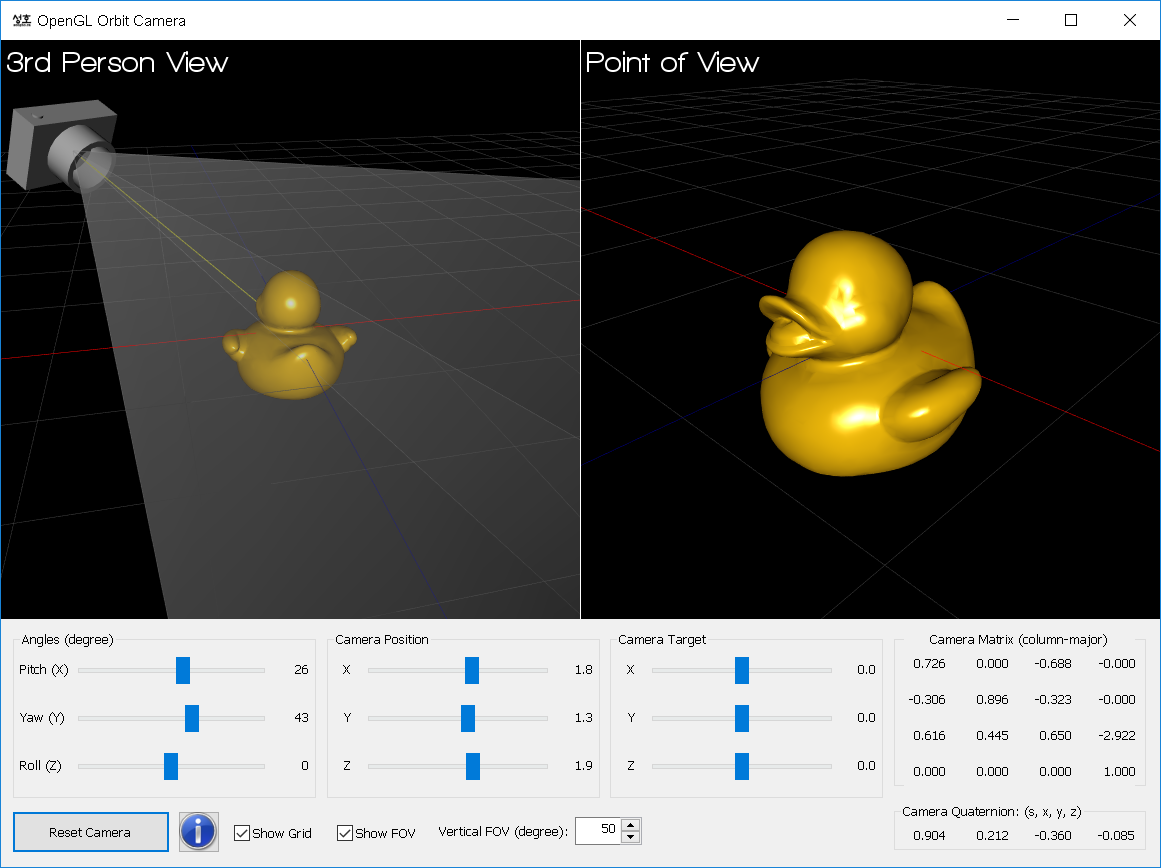
This GUI application visualizes various camera's transformations, such as lookat and rotations. Also, there is a WebGL JavaScript version of the orbit camera here.

Download source and binary:
(Updated: 2021-03-10)

OrbitCamera.zip (include VS 2015 project)

Example: Trackball

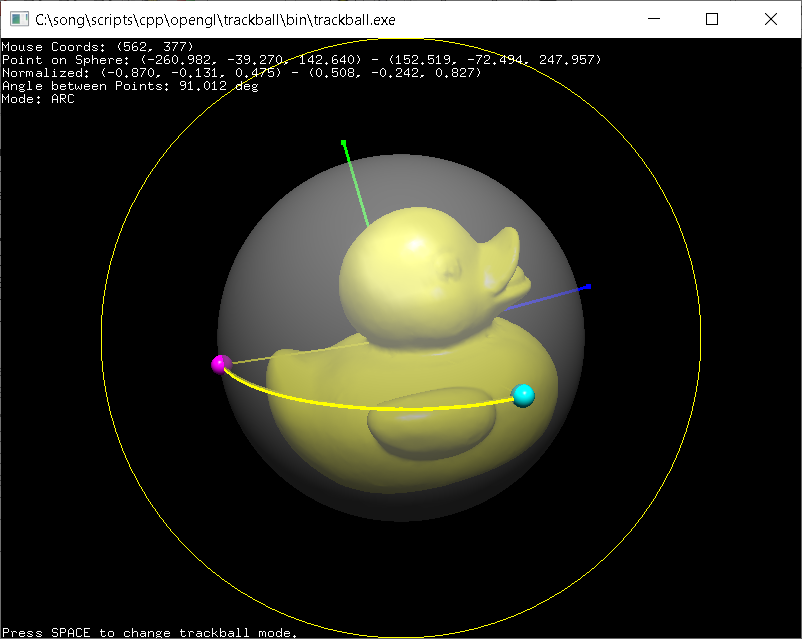
This demo application simulates an trackball style camera rotation by mapping the mouse cursor point of the screen space into a trackball (3D sphere) surface. It provides 2 different mapping modes; Arc and Project. See the detail implementation of C++ Trackball class and Quaternion.

Download: trackball.zip
(Updated 2024-03-24)

Reference: trackball.h / trackball.c by Gavin Bell at SGI.

© 2016 - 2024 Song Ho Ahn (안성호)